
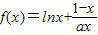 ,其中a为大于零的常数.
,其中a为大于零的常数. ,
, <a<1三种情况,分别讨论f′(x)的符号,分析出函数f(x)的单调性,进而可求出函数f(x)在区间[1,2]上的最小值.
<a<1三种情况,分别讨论f′(x)的符号,分析出函数f(x)的单调性,进而可求出函数f(x)在区间[1,2]上的最小值.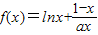 ,
, (x>0)…(2分)
(x>0)…(2分)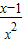 ,
, 时,f′(x)≤0恒成立,f(x)在[1,2]上单调递减,
时,f′(x)≤0恒成立,f(x)在[1,2]上单调递减, . …(10分)
. …(10分) <a<1时,由f′(x)>0得
<a<1时,由f′(x)>0得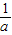 <x≤2,由f′(x)<0得1≤x<
<x≤2,由f′(x)<0得1≤x<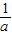 .
.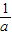 ]上单调递减,在[
]上单调递减,在[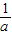 ,2]上单调递增.
,2]上单调递增.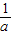 )=ln
)=ln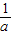 +1-
+1-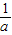 . …(14分)
. …(14分)

科目:高中数学 来源:黄冈中学 高一数学(下册)、第四章 三角函数单元(4.8~4.11)测试卷 题型:044
已知函数![]() ,其中a为实常数.
,其中a为实常数.
(1)若x∈R,求f(x)的最小正周期和单调递增区间;
(2)若![]() 时,f(x)的最大值为4,求a的值.
时,f(x)的最大值为4,求a的值.
查看答案和解析>>
科目:高中数学 来源:吉林省2009-2010学年第二学期期末考试高二年级数学科试卷 题型:解答题
已知函数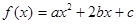 ,其中a≥b>c,a+b+c=0.
,其中a≥b>c,a+b+c=0.
(1)求证: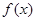 有两个零点;
有两个零点;
(2)若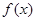 在
在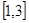 上的最小值为1,最大值为13,求a、b、c的值.
上的最小值为1,最大值为13,求a、b、c的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
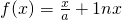 ,其中a为常数,e为自然对数的底数.
,其中a为常数,e为自然对数的底数.查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数![]() ,其中a为常数.
,其中a为常数.
(1) 当![]() 时,求
时,求![]() 的最大值;
的最大值;
(2) 若![]() 在区间(0,e]上的最大值为-3,求a的值;
在区间(0,e]上的最大值为-3,求a的值;
(3) 当![]() 时,试推断方程
时,试推断方程![]() =
=![]() 是否有实数解.
是否有实数解.
查看答案和解析>>
科目:高中数学 来源:2010年东北三省长春、哈尔滨、沈阳、大连第二次联考数学试卷(文科)(解析版) 题型:解答题
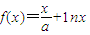 ,其中a为常数,e为自然对数的底数.
,其中a为常数,e为自然对数的底数.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com