
某市2010年4月1日—4月30日对空气污染指数的监测数据如下(主要污染物为可吸入颗粒物):
61,76,70,56,81,91,92,91,75,81,88,67,101,103,95,91,77,86,81,83,82,82,64,79,86,85,75,71,49,45.
(1)完成频率分布表;
(2)作出频率分布直方图;
(3)根据国家标准,污染指数在0~50之间时,空气质量为优;在51~100之间时,为良;在101~150之间时,为轻微污染;在151~200之间时,为轻度污染.
请你依据所给数据和上述标准,对该市的空气质量给出一个简短评价.
(1)频率分布表:
科目:高中数学
来源:
题型:解答题
为了了解某班的男女生学习体育的情况,按照分层抽样分别抽取了10名男生和5名女生作为样本,他们期末体育成绩的茎叶图如图所示,其中茎为十位数,叶为个位数。
科目:高中数学
来源:
题型:解答题
某校50名学生参加智力答题活动,每人回答3个问题,答对题目个数及对应人数统计结果见下表:
科目:高中数学
来源:
题型:解答题
甲、乙两人参加普法知识竞赛,共有10道不同的题目,其中选择题6道,判断题4道,甲、乙两人各抽一道(不重复).
科目:高中数学
来源:
题型:解答题
为了整顿道路交通秩序,某地考虑将对行人闯红灯进行处罚.为了了解市民的态度,在普通行人中随机选取了200人进行调查,得到如下数据:
科目:高中数学
来源:
题型:解答题
A、B两个试验方案在某科学试验中成功的概率相同,已知A、B两个方案至少一个方案试验成功的概率是0.36.
科目:高中数学
来源:
题型:解答题
因金融危机,某公司的出口额下降,为此有关专家提出两种促进出口的方案,每种方案都需要分两年实施。若实施方案一,预计第一年可以使出口额恢复到危机前的
科目:高中数学
来源:
题型:解答题
甲、乙、丙三人进行羽毛球练习赛,其中两人比赛,另一人当裁判,每局比赛结束时,负的一方在下一局当裁判.设各局中双方获胜的概率均为
科目:高中数学
来源:
题型:解答题
某厂生产的产品在出厂前都要做质量检测,每一件一等品都能通过检测,每一件二等品通过检测的概率为
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区分组 频数 频率 分组 频数 频率 [41,51) 2 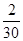
[81,91) 10 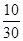
[51,61) 1 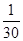
[91,101) 5 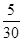
[61,71) 4 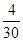
[101,111) 2 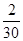
[71,81) 解析试题分析:(1)频率分布表: 分组 频数 频率 分组 频数 频率 [41,51) 2 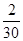
[81,91) 10 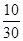
[51,61) 1 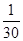
[91,101) 5 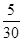
[61,71) 4 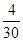
[101,111) 2 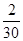
[71,81) 

新课程暑假作业广西师范大学出版社系列答案
高中暑假作业浙江教育出版社系列答案
少年素质教育报暑假作业系列答案
金太阳全A加系列答案
创新导学案新课标寒假假期自主学习训练系列答案
超能学典暑假接力棒江苏凤凰少年儿童出版社系列答案
暑假提高班系列答案
完美假期暑假作业系列答案
快乐假期高考状元假期学习方案暑假系列答案
豫欣图书自主课堂系列答案
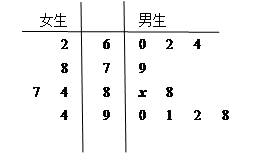
(Ⅰ)若该班男女生平均分数相等,求x的值;
(Ⅱ)若规定85分以上为优秀,在该10名男生中随机抽取2名,优秀的人数记为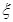 ,求
,求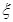 的分布列和数学期望.
的分布列和数学期望.
根据上表信息解答以下问题:答对题目个数
0
1
2
3
人数
5
10
20
15
(Ⅰ)从50名学生中任选两人,求两人答对题目个数之和为4或5的概率;
(Ⅱ)从50名学生中任选两人,用X表示这两名学生答对题目个数之差的绝对值,求随机变量X的分布列及数学期望EX.
(1)甲抽到选择题,乙抽到判断题的概率是多少?
(2)甲、乙二人中至少有一人抽到选择题的概率是多少?
若用表中数据所得频率代替概率.现从这5种处罚金额中随机抽取2种不同的金额进行处罚,在两个路口进行试验.处罚金额x(元)
0
5
10
15
20
会闯红灯的人数y
80
50
40
20
10
(Ⅰ)求这两种金额之和不低于20元的概率;
(Ⅱ)若用X表示这两种金额之和,求X的分布列和数学期望.
(1)求两个方案均获成功的概率;
(2)设试验成功的方案的个数为随机变量ξ,求ξ的分布列及数学期望. 倍、
倍、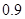 倍、
倍、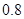 倍的概率分别为
倍的概率分别为 、
、 、
、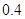 ;第二年可以使出口额为第一年的
;第二年可以使出口额为第一年的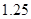 倍、
倍、 倍的概率分别为
倍的概率分别为 、
、 。若实施方案二,预计第一年可以使出口额恢复到危机前的
。若实施方案二,预计第一年可以使出口额恢复到危机前的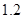 倍、
倍、 倍、
倍、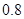 倍的概率分别为
倍的概率分别为 、
、 、
、 ;第二年可以使出口额为第一年的
;第二年可以使出口额为第一年的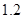 倍、
倍、 倍的概率分别为
倍的概率分别为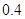 、
、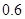 。实施每种方案第一年与第二年相互独立。令
。实施每种方案第一年与第二年相互独立。令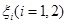 表示方案
表示方案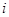 实施两年后出口额达到危机前的倍数。
实施两年后出口额达到危机前的倍数。
(1)写出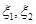 的分布列;
的分布列;
(2)实施哪种方案,两年后出口额超过危机前出口额的概率更大?
(3)不管哪种方案,如果实施两年后出口额达不到、恰好达到、超过危机前出口额,预计利润分别为 万元、
万元、 万元、
万元、 万元,问实施哪种方案的平均利润更大?
万元,问实施哪种方案的平均利润更大? ,各局比赛的结束相互独立,第1局甲当裁判.
,各局比赛的结束相互独立,第1局甲当裁判.
(Ⅰ)求第4局甲当裁判的概率;
(Ⅱ)X表示前4局中乙当裁判的次数,求X的数学期望.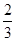 .现有10件产品,其中6件是一等品,4件是二等品.
.现有10件产品,其中6件是一等品,4件是二等品.
(1)随机选取1件产品,求能够通过检测的概率;
(2)随机选取3件产品,其中一等品的件数记为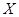 ,求
,求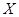 的分布列;
的分布列;
(3)随机选取3件产品,求这三件产品都不能通过检测的概率.
版权声明:本站所有文章,图片来源于网络,著作权及版权归原作者所有,转载无意侵犯版权,如有侵权,请作者速来函告知,我们将尽快处理,联系qq:3310059649。
ICP备案序号: 沪ICP备07509807号-10 鄂公网安备42018502000812号