(1) ,
,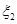 的分布列为:
的分布列为:

| 1.25
| 1.125
| 1
| 0.9
| 0.8
|
P
| 0.15
| 0.15
| 0.35
| 0.15
| 0.2
|
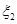
| 1.44
| 1.2
| 1
| 0.96
| 0.8
|
P
| 0.08
| 0.24
| 0.18
| 0.2
| 0.3
|
(2)实施方案二的概率更大
(3)第一个方案的平均利润更大
解析试题分析:(1) 根据题意,由于实施方案一,预计第一年可以使出口额恢复到危机前的 倍、
倍、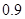 倍、
倍、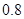 倍的概率分别为
倍的概率分别为 、
、 、
、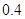 ;第二年可以使出口额为第一年的
;第二年可以使出口额为第一年的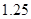 倍、
倍、 倍的概率分别为
倍的概率分别为 、
、 。若实施方案二,预计第一年可以使出口额恢复到危机前的
。若实施方案二,预计第一年可以使出口额恢复到危机前的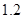 倍、
倍、 倍、
倍、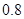 倍的概率分别为
倍的概率分别为 、
、 、
、 ;第二年可以使出口额为第一年的
;第二年可以使出口额为第一年的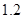 倍、
倍、 倍的概率分别为
倍的概率分别为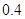 、
、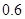 ,那么可知
,那么可知 ,
,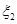 的分布列为:
的分布列为:

| 1.25
| 1.125
| 1
| 0.9
| 0.8
|
P
| 0.15
| 0.15
| 0.35
| 0.15
| 0.2
|
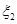
| 1.44
| 1.2
| 1
| 0.96
| 0.8
|
P
| 0.08
| 0.24
|
练习册系列答案
相关习题
科目:高中数学
来源:
题型:解答题
某小组共有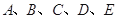 五位同学,他们的身高(单位:米)以及体重指标(单位:千克/米2)如下表所示: 五位同学,他们的身高(单位:米)以及体重指标(单位:千克/米2)如下表所示:
| A
| B
| C
| D
| E
| 身高
| 1.69
| 1.73
| 1.75
| 1.79
| 1.82
| 体重指标
| 19.2
| 25.1
| 18.5
| 23.3
| 20.9
|
(1)从该小组身高低于1.80的同学中任选2人,求选到的2人身高都在1.78以下的概率; (2)从该小组同学中任选2人,求选到的2人的身高都在1.70以上且体重指标都在[18.5,23.9)中的概率.
查看答案和解析>>
科目:高中数学
来源:
题型:解答题
通过随机询问某校110名高中学生在购买食物时是否看营养说明,得到如下的列联表:
性别与看营养说明列联表 单位: 名
| 男
| 女
| 总计
| 看营养说明
| 50
| 30
| 80
| 不看营养说明
| 10
| 20
| 30
| 总计
| 60
| 50
| 110
|
(1)从这50名女生中按是否看营养说明采取分层抽样,抽取一个容量为10的样本,问样本中看与不看营养说明的女生各有多少名? (2)根据以上列联表,能否在犯错误的概率不超过0.01的前提下认为性别与是否看营养说明之间有关系? 下面的临界值表供参考: 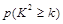
| 0.15
| 0.10
| 0.05
| 0.025
| 0.010
| 0.005
| 0.001
| 
| 2.072
| 2.706
| 3.841
| 5.024
| 6.635
| 7.879
| 10.828
|
(参考公式:  ,其中  ) 
查看答案和解析>>
科目:高中数学
来源:
题型:解答题
某商场经销某商品,根据以往资料统计,顾客采用的付款期数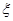 的分布列为 的分布列为
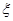
| 1
| 2
| 3
| 4
| 5
| 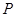
| 0.4
| 0.2
| 0.2
| 0.1
| 0.1
|
商场经销一件该商品,采用1期付款,其利润为200元;分2期或3期付款,其利润为250元;分4期或5期付款,其利润为300元.  表示经销一件该商品的利润. (Ⅰ)求事件 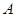 :“购买该商品的3位顾客中,至少有1位采用1期付款”的概率 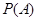 ; (Ⅱ)求  的分布列及期望 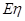 与方差D 
查看答案和解析>>
科目:高中数学
来源:
题型:解答题
某市2010年4月1日—4月30日对空气污染指数的监测数据如下(主要污染物为可吸入颗粒物):
61,76,70,56,81,91,92,91,75,81,88,67,101,103,95,91,77,86,81,83,82,82,64,79,86,85,75,71,49,45.
(1)完成频率分布表;
(2)作出频率分布直方图;
(3)根据国家标准,污染指数在0~50之间时,空气质量为优;在51~100之间时,为良;在101~150之间时,为轻微污染;在151~200之间时,为轻度污染.
请你依据所给数据和上述标准,对该市的空气质量给出一个简短评价.
查看答案和解析>>
科目:高中数学
来源:
题型:解答题
两枚质量均匀的正方体骰子,六个面上分别标有数字1、2、3、4、5、6,抛掷两枚骰子.记两枚骰子朝上的面上的数字分别为p,q,若把p,q分别作为点A的横坐标和纵坐标,
(1)用列表法或树状图表示出点A(p,q)所有可能出现的结果;
(2)求点A(p,q)在函数y=x-1的图象上的概率.
查看答案和解析>>
|

 倍、
倍、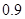 倍、
倍、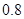 倍的概率分别为
倍的概率分别为 、
、 、
、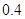 ;第二年可以使出口额为第一年的
;第二年可以使出口额为第一年的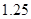 倍、
倍、 倍的概率分别为
倍的概率分别为 、
、 。若实施方案二,预计第一年可以使出口额恢复到危机前的
。若实施方案二,预计第一年可以使出口额恢复到危机前的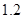 倍、
倍、 倍、
倍、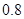 倍的概率分别为
倍的概率分别为 、
、 、
、 ;第二年可以使出口额为第一年的
;第二年可以使出口额为第一年的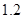 倍、
倍、 倍的概率分别为
倍的概率分别为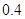 、
、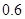 。实施每种方案第一年与第二年相互独立。令
。实施每种方案第一年与第二年相互独立。令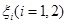 表示方案
表示方案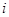 实施两年后出口额达到危机前的倍数。
实施两年后出口额达到危机前的倍数。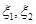 的分布列;
的分布列; 万元、
万元、 万元、
万元、 万元,问实施哪种方案的平均利润更大?
万元,问实施哪种方案的平均利润更大? ,
,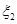 的分布列为:
的分布列为:
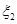
 倍、
倍、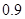 倍、
倍、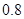 倍的概率分别为
倍的概率分别为 、
、 、
、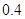 ;第二年可以使出口额为第一年的
;第二年可以使出口额为第一年的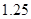 倍、
倍、 倍的概率分别为
倍的概率分别为 、
、 。若实施方案二,预计第一年可以使出口额恢复到危机前的
。若实施方案二,预计第一年可以使出口额恢复到危机前的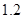 倍、
倍、 倍、
倍、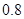 倍的概率分别为
倍的概率分别为 、
、 、
、 ;第二年可以使出口额为第一年的
;第二年可以使出口额为第一年的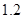 倍、
倍、 倍的概率分别为
倍的概率分别为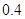 、
、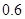 ,那么可知
,那么可知 ,
,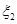 的分布列为:
的分布列为:
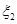


小学同步AB卷系列答案
新题型全程检测100分系列答案
新学考A加方案系列答案
状元大考卷系列答案
有效课堂课时作业本系列答案
芝麻开花王后雄状元考案系列答案
钟书金牌金试卷系列答案
领先AB卷系列答案
优化夺标系列答案
创新思维期末快递黄金8套系列答案
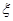 为取得红球的个数.
为取得红球的个数. 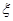 的分布列;
的分布列;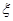 的数学期望
的数学期望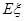 .
. 五位同学,他们的身高(单位:米)以及体重指标(单位:千克/米2)如下表所示:
五位同学,他们的身高(单位:米)以及体重指标(单位:千克/米2)如下表所示: 名工人,随机抽取
名工人,随机抽取 名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.
名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数. 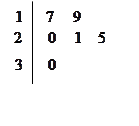
 名工人中有几名优秀工人;
名工人中有几名优秀工人; 名工人中,任取
名工人中,任取 人,求恰有
人,求恰有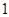 名优秀工人的概率.
名优秀工人的概率. 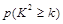

 ,其中
,其中 )
)
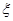 的分布列为
的分布列为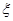
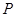
 表示经销一件该商品的利润.
表示经销一件该商品的利润.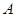 :“购买该商品的3位顾客中,至少有1位采用1期付款”的概率
:“购买该商品的3位顾客中,至少有1位采用1期付款”的概率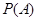 ;
; 的分布列及期望
的分布列及期望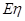 与方差D
与方差D
 小时收费
小时收费 元,超过
元,超过 小时的部分每小时收费
小时的部分每小时收费 元(不足
元(不足 小时的部分按
小时的部分按 小时计算).现有甲、乙二人在该商区临时停车,两人停车都不超过
小时计算).现有甲、乙二人在该商区临时停车,两人停车都不超过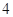 小时.
小时. 小时以上且不超过
小时以上且不超过 小时的概率为
小时的概率为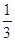 ,停车付费多于
,停车付费多于 元的概率为
元的概率为 ,求甲停车付费恰为
,求甲停车付费恰为 元的概率;
元的概率; 元的概率.
元的概率.