考点:函数单调性的性质
专题:函数的性质及应用
分析:根据题中条件,可以先判断出函数f(x)在R上单调递减,再结合分段函数的解析式,要每一段都是减函数,且分界点时左段函数的函数值要大于等于右段函数的函数值,列出不等关系,求解即可得到a的取值范围.
解答:
解:∵对任意x
1≠x
2都有
<0成立,
∴x
1-x
2与f(x
1)-f(x
2)异号,
根据函数单调性的定义,可知f(x)在R上是单调递减函数,
当x≥1时,f(x)=(a-3)x为减函数,则a-3<0,即a<3①,且x=1时,有最大值[(a-3)x]
max=a-3;
当x<1时,f(x)=x
2-2ax+2,为二次函数,图象开口向上,对称轴为x=a,若f(x)在(-∞,1)上为减函数,则对称轴在区间右侧,即a≥1②,且(x
2-2ax+2)
min>f(1)=3-2a;
又由题意函数在定义域R上单调递减,则(x
2-2ax+2)
min≥[(a-3)x]
max,即3-2a≥a-3,解得a≤2③;
综合①②③可得a的取值范围是1≤a≤2.
故答案为:1≤a≤2.
点评:本题考查了函数单调性的判断与证明,注意一般单调性的证明选用定义法证明,证明的步骤是:设值,作差,化简,定号,下结论.对于分段函数的问题,一般选用分类讨论和数形结合的思想方法进行求解.属于中档题.



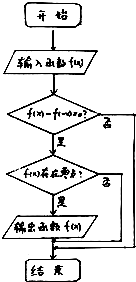 执行如图所示的程序框图,若输入如下四个函数①f(x)=sinx②f(x)=cosx③f(x)=e|x|④f(x)=|lnx|则输出的函数的个数为( )
执行如图所示的程序框图,若输入如下四个函数①f(x)=sinx②f(x)=cosx③f(x)=e|x|④f(x)=|lnx|则输出的函数的个数为( )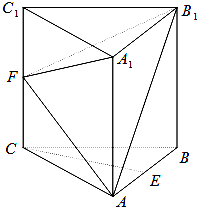 如图,在各棱长都相等的直三棱柱ABC-A1B1C1中,E,F分别为AB,CC1的中点.
如图,在各棱长都相等的直三棱柱ABC-A1B1C1中,E,F分别为AB,CC1的中点.