
【题目】已知正数数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() ,且
,且![]() .
.
(1)求![]() 的通项公式.
的通项公式.
(2)对任意![]() ,将数列
,将数列![]() 中落在区间
中落在区间![]() 内的项的项数记为
内的项的项数记为![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() .
.
【答案】(1) an=4n-3(n∈N*) (2) ![]()
【解析】
(1)利用递推关系与等差数列的通项公式即可得出;
(2)对任意m∈N+,4m<4n﹣3<42m,由![]() ,能求出数列{bm}的前m项和Sm.
,能求出数列{bm}的前m项和Sm.
(1) ∵![]() ,
,
∴8Sn﹣1![]() 4an﹣1+3,(n≥2),
4an﹣1+3,(n≥2),
∴![]() ,
,
∴![]()
∵an>0,∴an﹣an﹣1=4(n≥2),
∴数列{an}是以4为公差的等差数列.
又∵![]() ,
,
∴![]() ,而a1<3,
,而a1<3,
∴a1=1.
∴an=4n﹣3(n∈N*).
(2)对m∈N*,若4m<4n﹣3<42m
则4m+3<4n<42m+3.
因此![]() .
.
故得bm=![]() -
-![]() .
.
于是Sm=b1+b2+b3+…+bm
=(4+43+…+42m-1)-(1+4+…+4m-1)
![]() .
.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源: 题型:
【题目】由国家公安部提出,国家质量监督检验检疫总局发布的《车辆驾驶人员血液、呼气酒精含量阀值与检验标准(GB/T19522-2010)》于2011年7月1日正式实施.车辆驾驶人员酒饮后或者醉酒后驾车血液中的酒精含量阀值见表.经过反复试验,一般情况下,某人喝一瓶啤酒后酒精在人体血液中的变化规律的“散点图”见图,且图表示的函数模型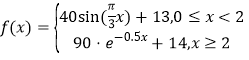 ,则该人喝一瓶啤酒后至少经过多长时间才可以驾车(时间以整小时计算)?(参考数据:
,则该人喝一瓶啤酒后至少经过多长时间才可以驾车(时间以整小时计算)?(参考数据:![]() ,
,![]() )
)
驾驶行为类型 | 阀值 |
饮酒后驾车 |
|
醉酒后驾车 |
|
车辆驾车人员血液酒精含量阀值
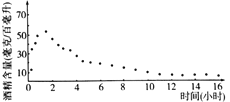
喝1瓶啤酒的情况
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若![]() ,求曲线
,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)若函数![]() 在其定义域内为增函数,求
在其定义域内为增函数,求![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,设函数![]() ,若在
,若在![]() 上至少存在一点
上至少存在一点![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 、
、![]() ,给定下列命题:(1)不等式
,给定下列命题:(1)不等式![]() 的解集为
的解集为![]() ;(2)函数
;(2)函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;(3)若函数
上单调递减;(3)若函数![]() 有两个极值点,则
有两个极值点,则![]() ;(4)若
;(4)若![]() 时,总有
时,总有![]() 恒成立,则
恒成立,则![]() 1.其中正确命题的序号为_________.
1.其中正确命题的序号为_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
![]() .
.
(1)若![]() 在
在![]() 处有极值,问是否存在实数m,使得不等式
处有极值,问是否存在实数m,使得不等式![]() 对任意
对任意![]() 及
及![]() 恒成立?若存在,求出m的取值范围;若不存在,请说明理由.
恒成立?若存在,求出m的取值范围;若不存在,请说明理由.![]() ;
;
(2)若![]() ,设
,设![]() .
.
①求证:当![]() 时,
时,![]() ;
;
②设![]() ,求证:
,求证:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知点A(0,﹣2),B(4,0),圆C经过点(0,﹣1),(0,1)及(![]() ,0).斜率为k的直线l经过点B.
,0).斜率为k的直线l经过点B.
(1)求圆C的标准方程;
(2)当k=2时,过直线l上的一点P向圆C引一条切线,切点为Q,且满足PQ=![]() ,求点P的坐标;
,求点P的坐标;
(3)设M,N是圆C上任意两个不同的点,若以MN为直径的圆与直线l都没有公共点,求k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com