
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 利用导数即可得出函数的极值点,再利用等差数列的性质及其对数的运算法则即可得出.
解答 解:函数f(x)=$\frac{1}{3}{x^3}-4{x^2}+6x-1$,可得f′(x)=x2-8x+6,
∵a1、a4031是函数f(x)=$\frac{1}{3}$x3-4x2+12x+1的极值点,
∴a1、a4031是方程x2-8x+12=0的两实数根,则a1+a4031=8.
数列{an}中,满足an+2=2an+1-an,
可知{an}为等差数列,
∴a1+a4031=2a2016,即a2016=4,
从而log2a2016=log24=2.
故选:A.
点评 熟练掌握利用导数研究函数的极值、等差数列的性质及其对数的运算法则是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
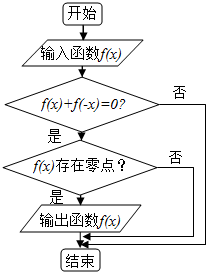 某程序据图如图所示,现输入如下四个函数:f(x)=x2,f(x)=$\frac{1}{x}$,f(x)=ex,f(x)=x3,则可以输出的函数( )
某程序据图如图所示,现输入如下四个函数:f(x)=x2,f(x)=$\frac{1}{x}$,f(x)=ex,f(x)=x3,则可以输出的函数( )| A. | f(x)=x2 | B. | f(x)=$\frac{1}{x}$ | C. | f(x)=ex | D. | f(x)=x3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x<-2015或0<x<2015} | B. | {x|x<-2015<x<0或x>2015} | ||
| C. | {x|x<-2015或x>2015} | D. | {x|-2015<x<0或0<x<2015} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (-∞,1] | C. | [1,+∞) | D. | φ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 支持 | 反对 | 总计 | |
| 男生 | 30 | ||
| 女生 | 25 | ||
| 总计 |
| P(K2≥k0) | 0.10 | 0.050 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706% | 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
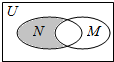 设全集U=R,M={x|x<-2,或x>2},N={x|1<x<3},则图中阴影部分所表示的集合是( )
设全集U=R,M={x|x<-2,或x>2},N={x|1<x<3},则图中阴影部分所表示的集合是( )| A. | {x|-2≤x<1} | B. | {x|-2≤x≤2} | C. | {x|1<x≤2} | D. | {x|x<2} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com