
(08年银川一中三模理)(12分) 已知椭圆C:![]() (a>b>0),点F1、F2分别是椭圆的左、右焦点,点P(2,
(a>b>0),点F1、F2分别是椭圆的左、右焦点,点P(2,![]() )在直线x=
)在直线x=![]() 上,且|F1F2|=|PF2|,直线
上,且|F1F2|=|PF2|,直线![]() :y=kx+m为动直线,且直线
:y=kx+m为动直线,且直线![]() 与椭圆C交于不同的两点A、B。
与椭圆C交于不同的两点A、B。
(Ⅰ)求椭圆C的方程;
(Ⅱ)若在椭圆C上存在点Q,满足![]() (O为坐标原点),求实数
(O为坐标原点),求实数![]() 的取值范围;
的取值范围;
(Ⅲ)在(Ⅱ)的条件下,当![]() 取何值时,△ABO的面积最大,并求出这个最大值.
取何值时,△ABO的面积最大,并求出这个最大值.
解析:椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() , ……2分
, ……2分
又![]() ,
,![]() ,
, ![]() ………3分
………3分
解得![]() ,
,
![]() 椭圆
椭圆![]() 的方程为
的方程为![]() . ………4分
. ………4分
(Ⅱ)由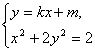 ,得
,得![]() .
.
设点![]() 、
、![]() 的坐标分别为
的坐标分别为![]() 、
、![]() ,则
,则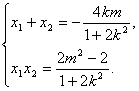 ……5分
……5分
![]() .
.
(1)当![]() 时,点
时,点![]() 、
、![]() 关于原点对称,则
关于原点对称,则![]() .
.
(2)当![]() 时,点
时,点![]() 、
、![]() 不关于原点对称,则
不关于原点对称,则![]() ,
,
由![]() ,得
,得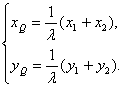 即
即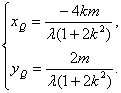
![]() 点
点![]() 在椭圆上,
在椭圆上,![]() 有
有![]() ,
,
化简,得![]() .
.
![]() ,
,![]() 有
有![]() .………………① ……………7分
.………………① ……………7分
又![]() ,
,
![]() 由
由![]() ,得
,得![]() .……………………………②
.……………………………②
将①、②两式,得![]() .
.
![]() ,
,![]() ,则
,则![]() 且
且![]() .
.
综合(1)、(2)两种情况,得实数![]() 的取值范围是
的取值范围是![]() . ………………8分
. ………………8分
(Ⅲ)![]() ,点
,点![]() 到直线
到直线![]() 的距离
的距离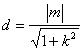 ,
,
![]() 的面积
的面积![]()
![]()
![]() . ………………………… 10分
. ………………………… 10分
由①有![]() ,代入上式并化简,得
,代入上式并化简,得![]() .
.
![]() ,
,![]() . ……………………… 11分
. ……………………… 11分
当且仅当![]() ,即
,即![]() 时,等号成立.
时,等号成立.
![]() 当
当![]() 时,
时,![]() 的面积最大,最大值为
的面积最大,最大值为![]() . ……………………… 12分
. ……………………… 12分


科目:高中数学 来源: 题型:
(08年银川一中三模文) (12分)现有编号分别为1,2,3,4,5的五个不同的物理题和编号分别为6,7,8,9的四个不同的化学题.甲同学从这九个题中一次随机抽取两道题,每题被抽到的概率是相等的,用符号 (x,y)表示事件“抽到的两题的编号分别为x、y,且x<y”.
(1)共有多少个基本事件?并列举出来;
(2)求甲同学所抽取的两题的编号之和小于17但不小于11的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年银川一中三模文)(12分) 已知椭圆C:![]() (a>b>0),点F1、F2分别是椭圆的左、右焦点,点P(2,
(a>b>0),点F1、F2分别是椭圆的左、右焦点,点P(2,![]() )在直线x=
)在直线x=![]() 上,且|F1F2|=|PF2|,直线
上,且|F1F2|=|PF2|,直线![]() :y=kx+m为动直线,且直线
:y=kx+m为动直线,且直线![]() 与椭圆C交于不同的两点A、B。
与椭圆C交于不同的两点A、B。
(Ⅰ)求椭圆C的方程;
(Ⅱ)若在椭圆C上存在点Q,满足![]() (O为坐标原点),求实数
(O为坐标原点),求实数![]() 的取值范围;
的取值范围;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com