已知定义在R上的函数f(x)=log2(x2+ax+5)(a>0),其值域为[2,+∞).
(1)求函数f(x)的解析式.
(2)讨论函数f(x)在区间[b,+∞)(b∈R)上的单调性.(写出完整解题过程)
解:(1)由题意函数f(x)=log
2(x
2+ax+5)在R上的最小值为2,
因为函数y=log
2u在(0,+∞)上是增函数,
所以当f(x)=log
2(x
2+ax+5)取最小值时,u=x
2+ax+5也取最小值
所以函数y=x
2+ax+5在R上的最小值为2
2=4,
得
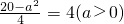
,解得a=2,
所以f(x)的解析式为f(x)=log
2(x
2+2x+5)
(2)因为y=log
2u在(0,+∞)上是增函数,
函数u=x
2+2x+5在(-∞,-1]上单调递减,在[-1,+∞)上单调递增
所以函数f(x)=log
2(x
2+ax+5)在在(-∞,-1]上单调递减,在[-1,+∞)上单调递增
所以,当b≥-1时,函数f(x)在区间[b,+∞)上单调递增
当b<-1时,函数f(x)在区间[b,-1]上单调递减,在[-1,+∞)上单调递增.
分析:(1)根据函数f(x)=log
2(x
2+ax+5)(a>0)的值域为[2,+∞),可知u=x
2+ax+5的最小值为4,x∈R,利用二次函数的最值求法,即可求得结果;
(2)欲求得函数f(x)=log
2(x
2+ax+5)在区间[b,+∞)(b∈R)上的单调性,将函数f(x)=log
2(x
2+ax+5)分解成两部分:f(U)=log
2U外层函数,U=x
2+ax+5是内层函数.外层函数是对数函数,其底数大于1,是(0,+∞)增函数,故要求函数f(x)在区间[b,+∞)(b∈R)上的单调性,即求函数U=x
2+ax+5在区间[b,+∞)上的单调性即可,注意分类讨论.
点评:本题考查与对数函数有关的复合函数的值域和单调性的判定,体现了分类讨论的数学思想,考查运算能力,属中档题.

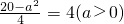 ,解得a=2,
,解得a=2,
