
| A. | 3 | B. | 4 | C. | 2$\sqrt{2}$ | D. | 3+2$\sqrt{2}$ |
分析 运用乘1法,可得$\frac{2}{x}$+$\frac{1}{y}$=(x+y)($\frac{2}{x}$+$\frac{1}{y}$)=3+$\frac{x}{y}$+$\frac{2y}{x}$,再由基本不等式计算即可得到所求最小值及相应x,y的值.
解答 解:正实数x、y满足x+y=1,可得:
$\frac{2}{x}$+$\frac{1}{y}$=(x+y)($\frac{2}{x}$+$\frac{1}{y}$)=3+$\frac{x}{y}$+$\frac{2y}{x}$≥3+2$\sqrt{\frac{x}{y}•\frac{2y}{x}}$=3+2$\sqrt{2}$.
当且仅当x=$\sqrt{2}$y=2-$\sqrt{2}$,取得最小值3+2$\sqrt{2}$.
故选:D.
点评 本题考查基本不等式的运用:求最值,注意运用乘1法和满足的条件:一正二定三等,考查运算能力,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 身高x(cm) | 160 | 165 | 170 | 175 | 180 |
| 体重y(kg) | 65 | 69 | m | 72 | 74 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{\frac{1}{2},+∞})$ | B. | $[{\frac{1}{4},+∞})$ | C. | $({-∞,\frac{1}{2}}]$ | D. | $({-∞,\frac{1}{4}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 一个几何体的三视图如图所示,若其正视图、侧视图的轮廓都是边长为1的菱形,俯视图是边长为1的正方形,则该几何体的体积为$\frac{\sqrt{3}}{3}$.
一个几何体的三视图如图所示,若其正视图、侧视图的轮廓都是边长为1的菱形,俯视图是边长为1的正方形,则该几何体的体积为$\frac{\sqrt{3}}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
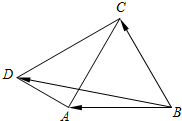 如图,在四边形ABCD中,△ABC是边长为6的正三角形,设$\overrightarrow{BD}=x\overrightarrow{BA}+y\overrightarrow{BC}$(x,y∈R).
如图,在四边形ABCD中,△ABC是边长为6的正三角形,设$\overrightarrow{BD}=x\overrightarrow{BA}+y\overrightarrow{BC}$(x,y∈R).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,BC=$\sqrt{2}$,AB=CC1=2,∠BCC1=$\frac{π}{4}$,点E在棱BB1上.
如图在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,BC=$\sqrt{2}$,AB=CC1=2,∠BCC1=$\frac{π}{4}$,点E在棱BB1上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com