
| A. | $[{\frac{1}{2},+∞})$ | B. | $[{\frac{1}{4},+∞})$ | C. | $({-∞,\frac{1}{2}}]$ | D. | $({-∞,\frac{1}{4}}]$ |
分析 根据题意,问题转化为s∈[-1,3],t∈[0,2]时,f(s)min≥g(t)min;求出对应的最小值,再解不等式即可.
解答 解:?x1∈[-1,3],?x2∈[0,2],f(x1)≥g(x2),
等价于s∈[-1,3],t∈[0,2],f(s)min≥g(t)min;
当s∈[-1,3]时,f(s)min=f(0)=0;
当t∈[0,2]时,$g{(t)_{min}}=g(2)=\frac{1}{4}-m$,
所以$0≥\frac{1}{4}-m$,
解得$m≥\frac{1}{4}$,
所以m的取值范围是[$\frac{1}{4}$,+∞).
故选:B.
点评 本题考查了指数函数的图象与性质的应用问题,也考查了转化思想的应用问题,是基础题目.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 2$\sqrt{2}$ | D. | 3+2$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ∅ | B. | {0,1} | C. | {-1,1} | D. | (-1,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
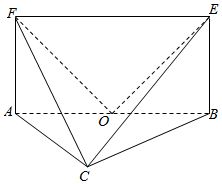 如图,平面ABEF⊥平面ABC,四边形ABEF为矩形,AC=BC.O为AB的中点,OF⊥EC.
如图,平面ABEF⊥平面ABC,四边形ABEF为矩形,AC=BC.O为AB的中点,OF⊥EC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
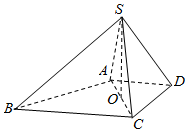 如图,在底面为梯形的四棱锥S-ABCD中,已知AD∥BC,∠ASC=60°,∠BAD=135°,AD=DC=$\sqrt{2}$,SA=SC=SD=2,O为AC中点.
如图,在底面为梯形的四棱锥S-ABCD中,已知AD∥BC,∠ASC=60°,∠BAD=135°,AD=DC=$\sqrt{2}$,SA=SC=SD=2,O为AC中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com