
����Ŀ����ͼ��ʾ��ij�ֵ���ί������EF�ضεľ���¥���Ϸ���Ŀհض�AE�Ͻ�һ������ģ�����AE��Ϊ30�ף�����Ķ������������¥ƽ�У��Ӷ�����������ĵĽ���ͼ���²����dz�����ABCD���ϲ�������DCΪֱ���İ�Բ��Ϊ�˱�֤����¥ס���IJɹ�Ҫ����������Բ���е�̫���������������ھ���¥�ϵ�Ӱ��GE������2.5�ף����и�̫��������ˮƽ�ߵļн�������tan ����![]() .
.

��1�������AB��18�ף�AD��6�ף����ܷ�֤�����ɹ�Ҫ��
��2���ڱ�֤�����ɹ�Ҫ���ǰ���£�������AB��AD�ij��ȣ���ʹ�û���ĵĽ��������� (ע����������ȡ3)
���𰸡���1���� ��2����AB��20����AD��5��ʱ����ʹ�û���ĵĽ���������
��������
��1���Ե�AΪ����ԭ�㣬AB����ֱ��Ϊx�ᣬ����ƽ��ֱ������ϵ����̫����������ֱ�߷���Ϊy=![]() x+b������ֱ����Բ���У����ֱ�߷��̣���x=30����EG=1.5�ף�2.5�ף���
x+b������ֱ����Բ���У����ֱ�߷��̣���x=30����EG=1.5�ף�2.5�ף���
�ɵó����ۣ���2����ʹ������ڲ��ռ価���ܴ���Ӱ��EGǡΪ2.5�ף������������������.
�⣺��ͼ����AΪ����ԭ�㣬AB����ֱ��Ϊx�ᣬ����ƽ��ֱ������ϵ��
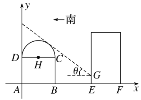
��1����ΪAB��18�ף�AD��6�ף�
����Բ��Բ��ΪH(9,6)���뾶r��9.
��̫����������ֱ�߷���Ϊy����![]() x��b��
x��b��
��3x��4y��4b��0������![]() ��9��
��9��
���b��24��b��![]() (��)��
(��)��
��̫����������ֱ�߷���Ϊy����![]() x��24,
x��24,
��x��30����EG��1.5��2.5.
���Դ�ʱ�ܱ�֤�����ɹ�Ҫ��
��2����AD��h�ף�AB��2r�ף�
���Բ��Բ��ΪH(r��h)���뾶Ϊr.
����һ����̫����������ֱ�߷���Ϊy����![]() x��b��
x��b��
��3x��4y��4b��0��
��![]() ��r�����b��h��2r��b��h��
��r�����b��h��2r��b��h��![]() (��)��
(��)��
��̫����������ֱ�߷���Ϊy����![]() x��h��2r��
x��h��2r��
��x��30����EG��2r��h��![]() ��
��
��EG��![]() ����h��25��2r.
����h��25��2r.
����S��2rh��![]() ��r2��2rh��
��r2��2rh��![]() ��r2��2r(25��2r)��
��r2��2r(25��2r)��![]() ��r2
��r2
����![]() r2��50r����
r2��50r����![]() (r��10)2��250��250.
(r��10)2��250��250.
���ҽ���r��10ʱȡ�Ⱥţ�
���Ե�AB��20����AD��5��ʱ��
��ʹ�û���ĵĽ���������
����������ʹ������ڲ��ռ価���ܴ�
��Ӱ��EGǡΪ2.5�ף����ʱ��GΪ(30,2.5)��
�����G������̫������Ϊl1��
��l1����ֱ�߷���Ϊy��![]() ����
����![]() (x��30)��
(x��30)��
��3x��4y��100��0.
��ֱ��l1���ԲH���У���r��![]() .
.
����H(r��h)��ֱ��l1���·�����3r��4h��100��0��
��r����![]() ���Ӷ�h��25��2r.
���Ӷ�h��25��2r.
��S��2rh��![]() ��r2��2r(25��2r)��
��r2��2r(25��2r)��![]() ��r2����
��r2����![]() r2��50r����
r2��50r����![]() (r��10)2��250��250.���ҽ���r��10ʱȡ�Ⱥţ�
(r��10)2��250��250.���ҽ���r��10ʱȡ�Ⱥţ�
���Ե�AB��20����AD��5��ʱ��
��ʹ�û���ĵĽ���������


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ���ͼ��ʾ�ij����ͼ��������a��ֵΪ ![]() ���������kֵ�ǣ� ��
���������kֵ�ǣ� �� 
A.9
B.10
C.11
D.12
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����y=x2��ͼ���ڵ㣨x0 �� x02����������Ϊl����lҲ�뺯��y=lnx��x�ʣ�0��1����ͼ�����У���x0�����㣨 ��
A.0��x0�� ![]()
B.![]() ��x0��1
��x0��1
C.![]() ��x0��
��x0�� ![]()
D.![]() ��x0
��x0 ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ֱ������ϵxOy�У�ԲC�IJ�������Ϊ ![]() ����Ϊ��������������ԭ��Ϊ���㣬x���������Ϊ���Ὠ��������ϵ��ֱ��l�ļ����귽��Ϊ
����Ϊ��������������ԭ��Ϊ���㣬x���������Ϊ���Ὠ��������ϵ��ֱ��l�ļ����귽��Ϊ ![]() ��
��
��1����ԲC����ͨ���̺�ֱ��l��ֱ�����귽�̣�
��2����M��ֱ��l������һ�㣬��M��ԲC���ߣ��е�ΪA��B�����ı���AMBC�������Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��f�䣨x�����溯��f��x����x��R���ĵ�������f����1��=0����x��0ʱ��xf�䣨x����f��x����0����ʹ��f��x����0������x��ȡֵ��Χ�ǣ� ��
A.�����ޣ���1���ȣ�0��1��
B.����1��0���ȣ�1��+�ޣ�
C.�����ޣ���1���ȣ���1��0��
D.��0��1���ȣ�1��+�ޣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ԲC�� ![]() =1��a��b��0������A
=1��a��b��0������A ![]() ��������Ϊ
��������Ϊ ![]() ����F1 �� F2�ֱ�Ϊ�����ҽ��㣮
����F1 �� F2�ֱ�Ϊ�����ҽ��㣮
��1������ԲC�ı����̣�
��2���Ƿ����Բ����ԭ���Բ��ʹ�ø�Բ������һ����������ԲC������������P��Q���� ![]() �������ڣ������Բ�ķ��̣��������ڣ���˵�����ɣ�
�������ڣ������Բ�ķ��̣��������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��f��x��=|x�� ![]() |+|x+m|��m��0��
|+|x+m|��m��0��
��1��֤����f��x����4��
��2����f��2����5����m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У�F����ԲP�� ![]() ��a��b��0�����ҽ��㣬��֪A��0����2������Բ�����ֱ��y=x�Գƣ���ֱ��AF��б��Ϊ
��a��b��0�����ҽ��㣬��֪A��0����2������Բ�����ֱ��y=x�Գƣ���ֱ��AF��б��Ϊ ![]() ��
��
��1������ԲP�ķ��̣�
��2������Q����1��0����ֱ��l����ԲP��M��N���㣬��ֱ��x=��4�ڵ�E�� ![]() =
= ![]() ��
�� ![]() =
= ![]() ��֤������+��Ϊ��ֵ��
��֤������+��Ϊ��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У���A��B��C�ĶԱ߷ֱ�Ϊa��b��c����a��b��c�� ![]() ��
��
��1����B�Ĵ�С��
��2����a=2�� ![]() ����c��ֵ��
����c��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com