Question

设．
（Ⅰ）若函数f（x）在区间（1，4）内单调递减，求a的取值范围；
（Ⅱ）若函数f（x）在x=a处取得极小值是1，求a的值，并说明在区间（1，4）内函数f（x）的单调性．

Answer 1

解：f'（x）=3x²-3（a+1）x+3a=3（x-1）（x-a）（2分）
（1）∵函数f（x）在区间（1，4）内单调递减，
∴f'（4）≤0，∴a∈[4，+∞）；（5分）
（2）∵函数f（x）在x=a处有极值是1，
∴f（a）=1，即，
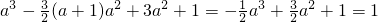
∴a²（a-3）=0，所以a=0或3，（8分）
当a=0时，f（x）在（-∞，0）上单调递增，在（0，1）上单调递减，
所以f（0）为极大值，这与函数f（x）在x=a处取得极小值是1矛盾，所以a¹0．（10分）
当a=3时，f（x）在（1，3）上单调递减，在（3，+∞）上单调递增，
所以f（3）为极小值，所以a=3．
此时，在区间（1，4）内函数f（x）的单调性是：f（x）在（1，3）内减，在[3，4）内增．
分析：（1）先求出导函数f'（x），然后根据函数f（x）在区间（1，4）内单调递减，则f'（4）≤0，可求出a的范围；
（2）根据函数f（x）在x=a处有极值是1，可知f（a）=1建立等式，解之即可求出a，然后将求出的a分别进行验证，从而求出在区间（1，4）内函数f（x）的单调性．
点评：本题主要考查导函数的正负与原函数的单调性之间的关系，即当导函数大于0时原函数单调递增，当导函数小于0时原函数单调递减，以及极值等有关知识，属于中档题．
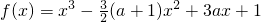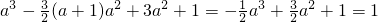