考点:命题的真假判断与应用
专题:空间位置关系与距离
分析:①根据线面平行的判断定理进行判断D1P∥平面A1BC1;
②D利用特殊值法即可判断D1P⊥BD不成立;
③根据面面垂直的判断条件即可判断平面PDB1⊥平面A1BC1;
④将三棱锥的体积进行等价转化,即可判断三棱锥A1-BPC1的体积不变.
解答:
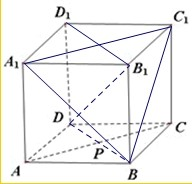
解:①∵在正方体中,D
1A∥BC
1,D
1C∥BA
1,且D
1A∩DC
1=D
1,
∴平面D
1AC∥平面A
1BC
1;
∵P在面对角线AC上运动,
∴D
1P∥平面A
1BC
1;∴①正确.
②当P位于AC的中点时,D
1P⊥BD不成立,∴②错误;
③∵A
1C
1⊥平面BDD
1B
1;∴A
1C
1⊥B
1D,
同理A
1B⊥B
1D,
∴B
1D⊥平面A
1BC
1,
∴平面BDD
1B⊥面ACD
1,
∴平面PDB
1⊥平面A
1BC
1;
∴③正确.
④三棱锥A
1-BPC
1的体积等于三棱锥B-A
1PC
1的体积.
△A
1PC
1的面积为定值
A1C1•AA1,
B到平面A
1PC
1的高为BP为定值,
∴三棱锥A
1-BPC
1的体积不变,∴④正确.
故答案为:①③④.
点评:本题主要考查空间直线和平面平行和垂直的位置关系的判断,综合考查学生的推理能力,综合性较强,难度较大.

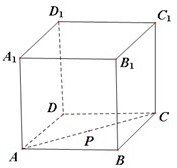 如图,在正方体ABCD-A1B1C1D1中,点P在面对角线AC上运动,给出下列四个命题:
如图,在正方体ABCD-A1B1C1D1中,点P在面对角线AC上运动,给出下列四个命题: 解:①∵在正方体中,D1A∥BC1,D1C∥BA1,且D1A∩DC1=D1,
解:①∵在正方体中,D1A∥BC1,D1C∥BA1,且D1A∩DC1=D1,