
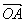
思路解析:OA⊥OB即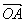 ·
·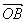 =0;OM⊥AB即
=0;OM⊥AB即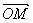 ·
·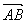 =0直接应用坐标运算即可.
=0直接应用坐标运算即可.
解:设A(![]() ,y1),B(
,y1),B(![]() ,y2),M(x,y).
,y2),M(x,y).
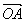 =(
=(![]() ,y1),
,y1),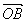 =(
=(![]() ,y2),
,y2),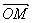 =(x,y),
=(x,y),
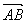 =(
=(![]() ,y2-y1),
,y2-y1),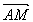 =(x-
=(x-![]() ,y-y1).
,y-y1).
∵OA⊥OB,∴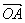 ·
·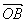 =0,即
=0,即![]() ·
·![]() +y1y2=0.∴y1y2=-16p2. ①
+y1y2=0.∴y1y2=-16p2. ①
又∵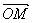 ⊥
⊥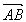 ,∴
,∴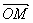 ·
· =0,即
=0,即![]() x+(y2-y1)y=0,
x+(y2-y1)y=0,
化简得![]() x+y=0. ②
x+y=0. ②
又∵AM∥AB,∴(x-![]() )(y2-y1)-(
)(y2-y1)-( ![]() -
-![]() )(y-y1)=0,
)(y-y1)=0,
即x-![]() ·y+
·y+![]() =0.把①、②代入整理得
=0.把①、②代入整理得
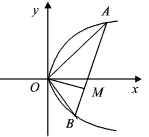
x2+y2-4px=0,∵A、B是异于原点的点,∴x≠0.
∴点M的轨迹方程为x2+y2-4px=0(x≠0),它表示以(2p,0)为圆心,以2p为半径的圆(除去原点).


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源:北京高考真题 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2000年北京市高考数学试卷(理)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com