
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 与圆
与圆![]() 相切,圆心
相切,圆心![]() 的坐标为
的坐标为![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)设直线![]() 与圆
与圆![]() 没有公共点,求
没有公共点,求![]() 的取值范围;
的取值范围;
(3)设直线![]() 与圆
与圆![]() 交于
交于![]() 、
、![]() 两点,且
两点,且![]() ,求
,求![]() 的值.
的值.
 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】已知![]() 的顶点坐标分别是
的顶点坐标分别是![]() ,
,![]() 的外接圆为
的外接圆为![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)在圆![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ?若存在,求点
?若存在,求点![]() 的个数:若不存在,说明理由;
的个数:若不存在,说明理由;
(3)在圆![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ?若存在,求点
?若存在,求点![]() 的个数:若不存在,说明理由.
的个数:若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校举行了一次考试,从学生中随机选取了![]() 人的成绩作为样本进行统计.已知这些学生的成绩全部在
人的成绩作为样本进行统计.已知这些学生的成绩全部在![]() 分至
分至![]() 分之间,现将成绩按如下方式分成
分之间,现将成绩按如下方式分成![]() 组:第一组
组:第一组![]() ,第二组
,第二组![]() ,.......,第六组
,.......,第六组![]() ,并据此绘制了如图所示的频率分布直方图.
,并据此绘制了如图所示的频率分布直方图.
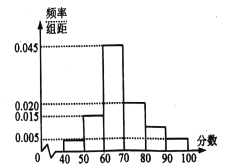
(1)估计这次月考数学成绩的平均分和众数;
(2)从成绩大于等于![]() 分的学生中随机抽取
分的学生中随机抽取![]() 人,求至少有
人,求至少有![]() 名学生的成绩在
名学生的成绩在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的离心率为
的离心率为![]() ,且经过点M(1,
,且经过点M(1,![]() ).
).
(1)求椭圆C的标准方程;
(2)已知直线l不过点P(0,1),与椭圆C交于A、B两点,记直线PA、PB的斜率分别为k1、k2,且满足k1+k2=1,求证:直线l过定点,并求出该定点坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)求证: ![]() .
.
(2)某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数:
sin213°+cos217°-sin13°cos17°;
sin215°+cos215°-sin15°cos15°;
sin218°+cos212°-sin18°cos12°;
sin2(-18°)+cos248°-sin(-18°)cos48°;
sin2(-25°)+cos255°-sin(-25°)cos55°.
①试从上述五个式子中选择一个,求出这个常数;
②根据①的计算结果,将该同学的发现推广为三角恒等式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“中国剩余定理”又称“孙子定理”.1852年英国来华传教士伟烈亚力将《孙子算经》中“物不知数”问题的解法传至欧洲.1874年英国数学家马西森指出此法符合1801年由高斯得到的关于同余式解法的一般性定理,因而西方称之为“中国剩余定理”,“中国剩余定理”讲的是一个关于整除的问题,现有这样一个整除问题:将1到2030这2030个自然数中,能被3除余1且被4除余1的数按从小到大的顺序排成一列,构成数列![]() ,则此数列共有( )
,则此数列共有( )
A.168项B.169项C.170项D.171项
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以
为参数),以![]() 轴的非负半轴为极轴,原点
轴的非负半轴为极轴,原点![]() 为极点建立极坐标系,两种坐标系中取相同的长度单位,若直线
为极点建立极坐标系,两种坐标系中取相同的长度单位,若直线![]() 和
和![]()
![]() 分别与曲线
分别与曲线![]() 相交于
相交于![]() 、
、![]() 两点(
两点(![]() ,
,![]() 两点异于坐标原点).
两点异于坐标原点).
(1)求曲线![]() 的普通方程与
的普通方程与![]() 、
、![]() 两点的极坐标;
两点的极坐标;
(2)求直线![]() 的极坐标方程及
的极坐标方程及![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的左焦点为
的左焦点为![]() ,离心率为
,离心率为![]() ,
,![]() 为圆
为圆![]() 的圆心.
的圆心.
(1)求椭圆的方程;
(2)已知过椭圆右焦点![]() 的直线
的直线![]() 交椭圆于
交椭圆于![]() 两点,过
两点,过![]() 且与
且与![]() 垂直的直线
垂直的直线![]() 与圆
与圆![]() 交于
交于![]() 两点,求四边形
两点,求四边形![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com