
【题目】已知![]() 的顶点坐标分别是
的顶点坐标分别是![]() ,
,![]() 的外接圆为
的外接圆为![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)在圆![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ?若存在,求点
?若存在,求点![]() 的个数:若不存在,说明理由;
的个数:若不存在,说明理由;
(3)在圆![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ?若存在,求点
?若存在,求点![]() 的个数:若不存在,说明理由.
的个数:若不存在,说明理由.
 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),曲线
为参数),曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)将![]() ,
, ![]() 的方程化为普通方程,并说明它们分别表示什么曲线?
的方程化为普通方程,并说明它们分别表示什么曲线?
(2)以坐标原点为极点,以![]() 轴的正半轴为极轴,建立极坐标系,已知直线
轴的正半轴为极轴,建立极坐标系,已知直线![]() 的极坐标方程为
的极坐标方程为![]() .若
.若![]() 上的点
上的点![]() 对应的参数为
对应的参数为![]() ,点
,点![]() 在
在![]() 上,点
上,点![]() 为
为![]() 的中点,求点
的中点,求点![]() 到直线
到直线![]() 距离的最小值.
距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年1月22日,国新办发布消息:新型冠状病毒来源于武汉一家海鲜市场非法销售的野生动.专家通过全基因组比对发现此病毒与2003年的非典冠状病毒以及此后的中东呼吸综合征冠状病毒,分别达到70%和40%的序列相似性.这种新型冠状病毒对人们的健康生命带来了严重威胁因此,某生物疫苗研究所加紧对新型冠状病毒疫苗进行实验,并将某一型号疫苗用在动物小白鼠身上进行科研和临床实验,得到统计数据如下:
未感染病毒 | 感染病毒 | 总计 | |
未注射疫苗 | 20 |
|
|
注射疫苗 | 30 |
|
|
总计 | 50 | 50 | 100 |
现从所有试验小白鼠中任取一只,取到“注射疫苗”小白鼠的概率为![]() .
.
(1)求![]() 列联表中的数据
列联表中的数据![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
(2)能否有99.9%把握认为注射此种疫苗对预防新型冠状病毒有效?
附:![]() .
.
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形![]() 垂直于直角梯形
垂直于直角梯形![]() ,
,![]() ,
,![]() 为
为![]() 中点,
中点,![]() ,
,![]() .
.
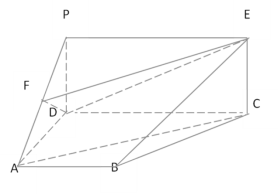
(1)求证:![]() ∥平面
∥平面![]() ;
;
(2)线段![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 与平面
与平面![]() 所成角的正切值为
所成角的正切值为![]() ?若存在,请求出
?若存在,请求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋子中放有大小和形状相同的小球若干,其中标号为0的小球1个,标号为1的小球1个,标号为2的小球n个,已知从袋子中随机抽取1个小球,取到标号为2的小球的概率是![]() .
.
(1)求n的值;
(2)从袋子中不放回地随机抽取2个球,记第一次取出小球标号为a,第二次取出的小球标号为b.①记“a+b=2”为事件A,求事件A的概率;
②在区间[0,2]内任取2个实数x,y,求事件“x2+y2>(a-b)2恒成立”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产某种产品的年固定成本为250万元,每生产x千件,需另投入成本为C(x),当年产量不足80千件时,C(x)=![]() x2+10x(万元).当年产量不小于80千件时,C(x)=51x+
x2+10x(万元).当年产量不小于80千件时,C(x)=51x+![]() -1 450(万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
-1 450(万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润L(x)(万元)关于年产量x(千件)的函数解析式;
(2)当年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 与圆
与圆![]() 相切,圆心
相切,圆心![]() 的坐标为
的坐标为![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)设直线![]() 与圆
与圆![]() 没有公共点,求
没有公共点,求![]() 的取值范围;
的取值范围;
(3)设直线![]() 与圆
与圆![]() 交于
交于![]() 、
、![]() 两点,且
两点,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com