
【题目】某工厂生产某种产品的年固定成本为250万元,每生产x千件,需另投入成本为C(x),当年产量不足80千件时,C(x)=![]() x2+10x(万元).当年产量不小于80千件时,C(x)=51x+
x2+10x(万元).当年产量不小于80千件时,C(x)=51x+![]() -1 450(万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
-1 450(万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润L(x)(万元)关于年产量x(千件)的函数解析式;
(2)当年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
【答案】(1)L(x)= ;(2)100千件.
;(2)100千件.
【解析】
(1)根据题意,分段求得函数的解析式,即可求得![]() ;
;
(2)根据(1)中所求,结合基本不等式,求得![]() 的最大值即可.
的最大值即可.
(1)因为每件商品售价为0.05万元,则x千件商品销售额为0.05×1 000x万元,
依题意得:
当0<x<80时,L(x)=(0.05×1 000x)-![]() -250=-
-250=-![]() +40x-250.
+40x-250.
当x≥80时,L(x)=(0.05×1 000x)-![]() -250=1 200-
-250=1 200-![]() .
.
所以L(x)=
(2)当0<x<80时,L(x)=-![]() +950.
+950.
此时,当x=60时,L(x)取得最大值L(60)=950万元.
当x≥80时,L(x)=1 200-![]() ≤1 200-2
≤1 200-2![]() =1 200-200=1 000.
=1 200-200=1 000.
此时x=![]() ,即x=100时,L(x)取得最大值1 000万元.
,即x=100时,L(x)取得最大值1 000万元.
由于950<1 000,
所以当年产量为100千件时,该厂在这一商品生产中所获利润最大,
最大利润为1 000万元.


 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:
【题目】有下列四个命题:
(1)“若![]() ,则
,则![]() ,
,![]() 互为倒数”的逆命题;
互为倒数”的逆命题;
(2)“面积相等的三角形全等”的否命题;
(3)“若![]() ,则
,则![]() 有实数解”的逆否命题;
有实数解”的逆否命题;
(4)“若![]() ,则
,则![]() ”的逆否命题.
”的逆否命题.
其中真命题为( )
A. (1)(2) B. (2)(3) C. (4) D. (1)(2)(3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 的顶点坐标分别是
的顶点坐标分别是![]() ,
,![]() 的外接圆为
的外接圆为![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)在圆![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ?若存在,求点
?若存在,求点![]() 的个数:若不存在,说明理由;
的个数:若不存在,说明理由;
(3)在圆![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ?若存在,求点
?若存在,求点![]() 的个数:若不存在,说明理由.
的个数:若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有3名男生、4名女生,在下列不同条件下,求不同的排列方法总数.
(1)选5人排成一排;
(2)排成前后两排,前排4人,后排3人;
(3)全体排成一排,甲不站排头也不站排尾;
(4)全体排成一排,女生必须站在一起;
(5)全体排成一排,男生互不相邻.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点,![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程与曲线
的普通方程与曲线![]() 直角坐标方程;
直角坐标方程;
(2)设![]() 为曲线
为曲线![]() 上的动点,求点
上的动点,求点![]() 到
到![]() 上点的距离的最小值,并求此时点
上点的距离的最小值,并求此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】丹麦数学家琴生(Jensen)是19世纪对数学分析做出卓越贡献的巨人,特别是在函数的凸凹性与不等式方面留下了很多宝贵的成果,设函数![]() 在
在![]() 上的导函数为
上的导函数为![]() ,
,![]() 在
在![]() 上的导函数为
上的导函数为![]() ,若在
,若在![]() 上
上![]() 恒成立,则称函数
恒成立,则称函数![]() 在
在![]() 上为“凸函数”,已知
上为“凸函数”,已知![]() 在
在![]() 上为“凸函数”,则实数
上为“凸函数”,则实数![]() 的取值范围是__________.
的取值范围是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校举行了一次考试,从学生中随机选取了![]() 人的成绩作为样本进行统计.已知这些学生的成绩全部在
人的成绩作为样本进行统计.已知这些学生的成绩全部在![]() 分至
分至![]() 分之间,现将成绩按如下方式分成
分之间,现将成绩按如下方式分成![]() 组:第一组
组:第一组![]() ,第二组
,第二组![]() ,.......,第六组
,.......,第六组![]() ,并据此绘制了如图所示的频率分布直方图.
,并据此绘制了如图所示的频率分布直方图.
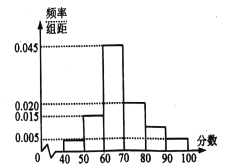
(1)估计这次月考数学成绩的平均分和众数;
(2)从成绩大于等于![]() 分的学生中随机抽取
分的学生中随机抽取![]() 人,求至少有
人,求至少有![]() 名学生的成绩在
名学生的成绩在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以
为参数),以![]() 轴的非负半轴为极轴,原点
轴的非负半轴为极轴,原点![]() 为极点建立极坐标系,两种坐标系中取相同的长度单位,若直线
为极点建立极坐标系,两种坐标系中取相同的长度单位,若直线![]() 和
和![]()
![]() 分别与曲线
分别与曲线![]() 相交于
相交于![]() 、
、![]() 两点(
两点(![]() ,
,![]() 两点异于坐标原点).
两点异于坐标原点).
(1)求曲线![]() 的普通方程与
的普通方程与![]() 、
、![]() 两点的极坐标;
两点的极坐标;
(2)求直线![]() 的极坐标方程及
的极坐标方程及![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com