Question

【题目】市积极倡导学生参与绿色环保活动，其中代号为“环保卫士－”的绿色环保活动小组对年月－年月(一月)内空气质量指数进行监测，如表是在这一年随机抽取的天的统计结果：

指数
空气质量	优	良	轻微污染	轻微污染	中度污染	中重度污染	重度污染
天数	4	13	18	30	9	11	15

（Ⅰ）若市某企业每天由空气污染造成的经济损失(单位：元)与空气质量指数(记为)的关系为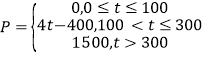：，，在这一年内随机抽取一天，估计该天经济损失元的概率；

（Ⅱ）若本次抽取的样本数据有天是在供暖季节，其中有天为重度污染，完成列联表，并判断是否有的把握认为市本年度空气重度污染与供暖有关？

下面临界值表供参考.

	0.15	0.10	0.05	0.010	0.005	0.001
	2.072	2.706	3.841	6.635	7.879	10.828

参考公式：.

Answer 1

【答案】（Ⅰ）.

（Ⅱ）

	非重度污染	重度污染	合计
供暖季	22	8	30
非供暖季	63	7	70
合计	85	15	100

有的把握认为市本年度空气重度污染与供暖有关．

【解析】分析：（Ⅰ）根据经济损失求出t的范围，根据t的范围，求出相应的天数，与总天数作比即可求出概率；

（Ⅱ）根据重度污染天数与供暖天数等求出各值，填入列联表，根据公式计算，与所对应的的k值3.841对比，若大，则有把握，否则没有.

详解：（Ⅰ）设“在本年内随机抽取一天，该天经济损失元”为事件.

由，得，频数为，

∴.

（Ⅱ）根据以上数据得到如表：

	非重度污染	重度污染	合计
供暖季	22	8	30
非供暖季	63	7	70
合计	85	15	100

的观测值

所以有的把握认为市本年度空气重度污染与供暖有关．