
【题目】已知函数![]() ,其中
,其中![]() ,
,![]() 为自然对数的底数.
为自然对数的底数.
(1)讨论![]() 的单调性;
的单调性;
(2)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的最大值.
上的最大值.
【答案】(1)见解析;(2)![]()
【解析】分析:(1)求出导函数![]() ,对
,对![]() 按
按![]() 和
和![]() 分类后可确定
分类后可确定![]() 的正负,即得
的正负,即得![]() 的单调区间;
的单调区间;
(2)由(1)![]() 的极值点是
的极值点是![]() ,因此在
,因此在![]() 时,函数在
时,函数在![]() 上单调递增,当
上单调递增,当![]() 时,可证
时,可证![]() (用导数的知识证明),然后比较
(用导数的知识证明),然后比较![]() 和
和![]() 的大小,最终求得最大值.
的大小,最终求得最大值.
详解:(1)![]() ,
,![]() .
.
当![]() 时,
时,![]() ,则
,则![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,令
时,令![]() ,得
,得![]() .
.
当![]() 时,
时,![]() ,
,![]() 单调递减;当
单调递减;当![]() 时,
时,![]() ,
,![]() 单调递增.
单调递增.
综上,当![]() 时,
时,![]() 在
在![]() 上单调递增;当
上单调递增;当![]() 时,
时,![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增.
单调递增.
(2)![]() ,令
,令![]() ,则
,则![]() .
.
当![]() 时,
时,![]() ,由(1)的结论可知函数
,由(1)的结论可知函数![]() 在
在![]() 上单调递增,
上单调递增,![]() .
.
当![]() 时,
时,![]() ,下证
,下证![]() .事实上,令
.事实上,令![]() ,
,
则![]() .当
.当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 为增函数,且
为增函数,且
![]() ,即当
,即当![]() 时,
时,![]() 恒成立.
恒成立.
由(1)的结论,知![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增.
单调递增.
所以![]() 在
在![]() 上的最大值等于
上的最大值等于![]() .
.
设![]() ,则
,则![]()
令![]() ,易得
,易得![]() ,因为
,因为![]() ,且
,且![]() 在
在![]() 恒成立,所以
恒成立,所以![]() 在
在![]() 单调递增,所以
单调递增,所以![]() ,即
,即![]() 恒成立,所以
恒成立,所以![]() 在在
在在![]() 上单调递增,所以
上单调递增,所以![]() 在
在![]() 上成立,即
上成立,即![]() .因此,当
.因此,当![]() 时,
时,![]() 在
在![]() 上的最大值为
上的最大值为![]() .
.
综上所述,当![]() 时,
时,![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】![]() 市积极倡导学生参与绿色环保活动,其中代号为“环保卫士-
市积极倡导学生参与绿色环保活动,其中代号为“环保卫士-![]() ”的绿色环保活动小组对
”的绿色环保活动小组对![]() 年
年![]() 月-
月-![]() 年
年![]() 月(一月)内空气质量指数
月(一月)内空气质量指数![]() 进行监测,如表是在这一年随机抽取的
进行监测,如表是在这一年随机抽取的![]() 天的统计结果:
天的统计结果:
指数 |
|
|
|
|
|
|
|
空气质量 | 优 | 良 | 轻微污染 | 轻微污染 | 中度污染 | 中重度污染 | 重度污染 |
天数 | 4 | 13 | 18 | 30 | 9 | 11 | 15 |
(Ⅰ)若![]() 市某企业每天由空气污染造成的经济损失
市某企业每天由空气污染造成的经济损失![]() (单位:元)与空气质量指数
(单位:元)与空气质量指数![]() (记为
(记为![]() )的关系为:
)的关系为: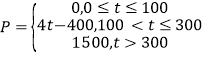 ,,在这一年内随机抽取一天,估计该天经济损失
,,在这一年内随机抽取一天,估计该天经济损失![]() 元的概率;
元的概率;
(Ⅱ)若本次抽取的样本数据有![]() 天是在供暖季节,其中有
天是在供暖季节,其中有![]() 天为重度污染,完成
天为重度污染,完成![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为
的把握认为![]() 市本年度空气重度污染与供暖有关?
市本年度空气重度污染与供暖有关?

下面临界值表供参考.
| 0.15 | 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
参考公式:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,动点M到两定点A(﹣1,0)、B(2,0)构成△MAB,且∠MBA=2∠MAB,设动点M的轨迹为C. 
(1)求轨迹C的方程;
(2)设直线y=﹣2x+m与y轴交于点P,与轨迹C相交于点Q、R,且|PQ|<|PR|,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 总决赛采用7场4胜制,2018年总决赛两支球队分别为勇士和骑士,假设每场比赛勇士获胜的概率为0.7,骑士获胜的概率为0.3,且每场比赛的结果相互独立,则恰好5场比赛决出总冠军的概率为__________.
总决赛采用7场4胜制,2018年总决赛两支球队分别为勇士和骑士,假设每场比赛勇士获胜的概率为0.7,骑士获胜的概率为0.3,且每场比赛的结果相互独立,则恰好5场比赛决出总冠军的概率为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合![]() ,其中
,其中![]() .
.
(1)写出集合![]() 中的所有元素;
中的所有元素;
(2)设![]() ,证明“
,证明“![]() ”的充要条件是“
”的充要条件是“![]() ”
”
(3)设集合![]() ,设
,设![]() ,使得
,使得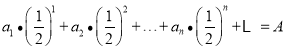 ,且
,且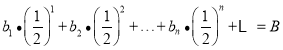 ,试判断“
,试判断“![]() ”是“
”是“![]() ”的什么条件并说明理由.
”的什么条件并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设{an}是公比不为1的等比数列,其前n项和为Sn , 且a5 , a3 , a4成等差数列.
(1)求数列{an}的公比;
(2)证明:对任意k∈N+ , Sk+2 , Sk , Sk+1成等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图 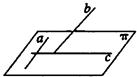
(1)证明命题“a是平面π内的一条直线,b是π外的一条直线(b不垂直于π),c是直线b在π上的投影,若a⊥b,则a⊥c”为真.
(2)写出上述命题的逆命题,并判断其真假(不需要证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
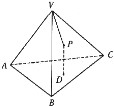
【题目】如图,P是正四面体V-ABC的面VBC上一点,点P到平面ABC距离与到点V的距离相等,则动点P的轨迹是( )
A. 直线 B. 抛物线
C. 离心率为![]() 的椭圆 D. 离心率为3的双曲线
的椭圆 D. 离心率为3的双曲线
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)若函数f(x)=ax2-x-1有且仅有一个零点, 求实数a的值.
(2)若函数f(x)=|4x-x2|+a有4个零点,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com