
【题目】如图 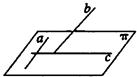
(1)证明命题“a是平面π内的一条直线,b是π外的一条直线(b不垂直于π),c是直线b在π上的投影,若a⊥b,则a⊥c”为真.
(2)写出上述命题的逆命题,并判断其真假(不需要证明)
【答案】
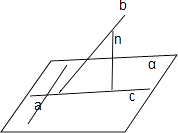
(1)证明:证法一:如图,过直线b上任一点作平面α的垂线n,设直线a,b,c,n对应的方向向量分别是 ![]() ,则
,则 ![]() 共面,
共面,
根据平面向量基本定理,存在实数λ,μ使得 ![]() ,
,
则 ![]() =
= ![]()
因为a⊥b,所以 ![]() ,
,
又因为aα,n⊥α,
所以 ![]() ,
,
故 ![]() ,从而a⊥c
,从而a⊥c
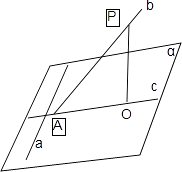
证法二
如图,记c∩b=A,P为直线b上异于点A的任意一点,过P做PO⊥π,垂足为O,则O∈c,
∵PO⊥π,aπ,
∴直线PO⊥a,
又a⊥b,b平面PAO,PO∩b=P,
∴a⊥平面PAO,
又c平面PAO,
∴a⊥c
(2)证明:逆命题为:a是平面π内的一条直线,b是π外的一条直线(b不垂直于π),c是直线b在π上的投影,若a⊥c,则a⊥b,
逆命题为真命题
【解析】(1)证法一:做出辅助线,在直线上构造对应的方向向量,要证两条直线垂直,只要证明两条直线对应的向量的数量积等于0,根据向量的运算法则得到结果.
证法二:做出辅助线,根据线面垂直的性质,得到线线垂直,根据线面垂直的判定定理,得到线面垂直,再根据性质得到结论.(2)把所给的命题的题设和结论交换位置,得到原命题的逆命题,判断出你命题的正确性.
【考点精析】通过灵活运用四种命题和向量语言表述线线的垂直、平行关系,掌握原命题:若P则q; 逆命题:若q则p;否命题:若┑P则┑q;逆否命题:若┑q则┑p;设直线![]() 的方向向量分别是
的方向向量分别是![]() ,则要证明
,则要证明![]() ∥
∥![]() ,只需证明
,只需证明![]() ∥
∥![]() ,即
,即![]() ;则要证明
;则要证明![]() ,只需证明
,只需证明![]() ,即
,即![]() 即可以解答此题.
即可以解答此题.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源: 题型:
【题目】海事救援船对一艘失事船进行定位:以失事船的当前位置为原点,以正北方向为y轴正方向建立平面直角坐标系(以1海里为单位长度),则救援船恰好在失事船正南方向12海里A处,如图,现假设: 
①失事船的移动路径可视为抛物线 ![]() ;
;
②定位后救援船即刻沿直线匀速前往救援;
③救援船出发t小时后,失事船所在位置的横坐标为7t
(1)当t=0.5时,写出失事船所在位置P的纵坐标,若此时两船恰好会合,求救援船速度的大小和方向.
(2)问救援船的时速至少是多少海里才能追上失事船?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lg(1-x)+lg(1+x)+x4-2x2.
(1)求函数f(x)的定义域;
(2)判断函数f(x)的奇偶性;
(3)求函数f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了解高二学生![]() 、
、![]() 两个学科学习成绩的合格情况是否有关,随机抽取了该年级一次期末考试
两个学科学习成绩的合格情况是否有关,随机抽取了该年级一次期末考试![]() 、
、![]() 两个学科的合格人数与不合格人数,得到以下2
两个学科的合格人数与不合格人数,得到以下2![]() 2列联表:
2列联表:
|
| 合计 | |
| 40 | 20 | 60 |
| 20 | 30 | 50 |
合计 | 60 | 50 | 110 |
(1)据此表格资料,能否在犯错的概率不超过0.01的前提下认为“![]() 学科合格”与“
学科合格”与“![]() 学科合格”有关;
学科合格”有关;
(2)从“![]() 学科合格”的学生中任意抽取2人,记被抽取的2名学生中“
学科合格”的学生中任意抽取2人,记被抽取的2名学生中“![]() 学科合格”的人数为
学科合格”的人数为![]() ,求
,求![]() 的数学期望.
的数学期望.
附公式与表:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
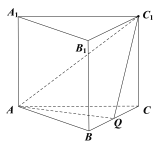
【题目】如图,在正三棱柱(底面为正三角形的直棱柱)ABC-A1B1C1中,已知AB=AA1=2,点Q为BC的中点.
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求点![]() 到平面AQC1的距离.
到平面AQC1的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,从A1(1,0,0),A2(2,0,0),B1(0,1,0),B2(0,2,0),C1(0,0,1),C2(0,0,2)这6个点中随机选取3个点,将这3个点及原点O两两相连构成一个“立体”,记该“立体”的体积为随机变量V(如果选取的3个点与原点在同一个平面内,此时“立体”的体积V=0).

(1)求V=0的概率;
(2)求V的分布列及数学期望E(V).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com