
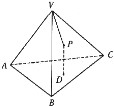
【题目】如图,P是正四面体V-ABC的面VBC上一点,点P到平面ABC距离与到点V的距离相等,则动点P的轨迹是( )
A. 直线 B. 抛物线
C. 离心率为![]() 的椭圆 D. 离心率为3的双曲线
的椭圆 D. 离心率为3的双曲线
【答案】C
【解析】分析:由题设条件将点P到平面ABC距离与到点V的距离相等转化成在面VBC中点P到V的距离与到定直线BC的距离比是一个常数,依据圆锥曲线的第二定义判断出其轨迹的形状.
详解:∵正四面体V﹣ABC∴面VBC不垂直面ABC,过P作PD⊥面ABC于D,过D作DH⊥BC于H,连接PH,
可得BC⊥面DPH,所以BC⊥PH,故∠PHD为二面角V﹣BC﹣A的平面角令其为θ
则Rt△PGH中,|PD|:|PH|=sinθ(θ为V﹣BC﹣A的二面角的大小).
又点P到平面ABC距离与到点V的距离相等,即|PV|=|PD|
∴|PV|:|PH|=sinθ<1,即在平面VBC中,点P到定点V的距离与定直线BC的距离之比是一个常数sinθ,
又在正四面体V﹣ABC,V﹣BC﹣A的二面角的大小θ有:sinθ=![]() <1,
<1,
由椭圆定义知P点轨迹为椭圆在面SBC内的一部分.
故答案为:C.


 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中数学 来源: 题型:
【题目】某居民小区有两个相互独立的安全防范系统(简称系统)A和B,系统A和B在任意时刻发生故障的概率分别为 ![]() 和p.
和p.
(1)若在任意时刻至少有一个系统不发生故障的概率为 ![]() ,求p的值;
,求p的值;
(2)设系统A在3次相互独立的检测中不发生故障的次数为随机变量ξ,求ξ的概率分布列及数学期望Eξ.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了解高二学生![]() 、
、![]() 两个学科学习成绩的合格情况是否有关,随机抽取了该年级一次期末考试
两个学科学习成绩的合格情况是否有关,随机抽取了该年级一次期末考试![]() 、
、![]() 两个学科的合格人数与不合格人数,得到以下2
两个学科的合格人数与不合格人数,得到以下2![]() 2列联表:
2列联表:
|
| 合计 | |
| 40 | 20 | 60 |
| 20 | 30 | 50 |
合计 | 60 | 50 | 110 |
(1)据此表格资料,能否在犯错的概率不超过0.01的前提下认为“![]() 学科合格”与“
学科合格”与“![]() 学科合格”有关;
学科合格”有关;
(2)从“![]() 学科合格”的学生中任意抽取2人,记被抽取的2名学生中“
学科合格”的学生中任意抽取2人,记被抽取的2名学生中“![]() 学科合格”的人数为
学科合格”的人数为![]() ,求
,求![]() 的数学期望.
的数学期望.
附公式与表:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,其中
,其中![]() ,
,![]() .
.
(1)设![]() ,若函数
,若函数![]() 的图象的一条对称轴为直线
的图象的一条对称轴为直线![]() ,求
,求![]() 的值;
的值;
(2)若将![]() 的图象向左平移
的图象向左平移![]() 个单位,或者向右平移
个单位,或者向右平移![]() 个单位得到的图象都过坐标原点,求所有满足条件的
个单位得到的图象都过坐标原点,求所有满足条件的![]() 和
和![]() 的值;
的值;
(3)设![]() ,
,![]() ,已知函数
,已知函数![]() 在区间
在区间![]() 上的所有零点依次为
上的所有零点依次为![]() ,且
,且![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
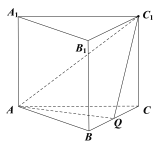
【题目】如图,在正三棱柱(底面为正三角形的直棱柱)ABC-A1B1C1中,已知AB=AA1=2,点Q为BC的中点.
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求点![]() 到平面AQC1的距离.
到平面AQC1的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设全集I={1,2,3,4,5,6},集合A,B都是I的子集,若A![]() B={1,3,5},则称A,B为“理想配集”,记作(A,B),问这样的“理想配集”(A,B)共有( )
B={1,3,5},则称A,B为“理想配集”,记作(A,B),问这样的“理想配集”(A,B)共有( )
A. 7个 B. 8个 C. 27个 D. 28个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com