
已知函数f(x)=Acos(ωx+φ)+b(A>0,ω>0,|φ|<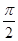 )在同一个周期内的图象上有一个最大值点A
)在同一个周期内的图象上有一个最大值点A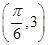 和一个最小值点B
和一个最小值点B .
.
(1)求f(x)的解析式;
(2)经过怎样的平移和伸缩变换可以将f(x)的图象变换为g(x)=cosx的图象.
(1)f(x)=4cos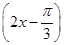 -1.(2)(一)将f(x)图象上各点向上平移1个单位;(二)将所得图象上各点横坐标伸长到原来的2倍,纵坐标缩短到原来的
-1.(2)(一)将f(x)图象上各点向上平移1个单位;(二)将所得图象上各点横坐标伸长到原来的2倍,纵坐标缩短到原来的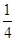 ;(三)将所得图象上各点左移
;(三)将所得图象上各点左移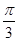 个单位,即可得到g(x)=cosx的图象.
个单位,即可得到g(x)=cosx的图象.
【解析】 (1)由f(x)的最大值点A与最小值点B可知,A=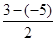 =4,b=
=4,b=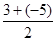 =-1,
=-1,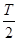 =
=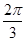 -
-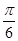 =
=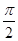 ,∴T=
,∴T=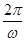 =π,∴ω=2.∴f(x)=4cos(2x+φ)-1.
=π,∴ω=2.∴f(x)=4cos(2x+φ)-1.
将点A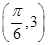 代入得:4cos
代入得:4cos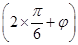 -1=3,
-1=3,
∴cos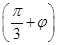 =1,
=1,
∴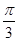 +φ=2kπ (k∈Z),∴φ=2kπ-
+φ=2kπ (k∈Z),∴φ=2kπ-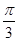 ,
,
∵|φ|<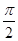 ,∴φ=-
,∴φ=-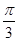 ,∴f(x)=4cos
,∴f(x)=4cos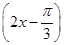 -1.
-1.
(2)依次按下列步骤变换:(一)将f(x)图象上各点向上平移1个单位;(二)将所得图象上各点横坐标伸长到原来的2倍,纵坐标缩短到原来的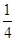 ;(三)将所得图象上各点左移
;(三)将所得图象上各点左移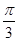 个单位,即可得到g(x)=cosx的图象.
个单位,即可得到g(x)=cosx的图象.


科目:高中数学 来源:2012-2013学年江西省南昌市高一5月联考数学卷(解析版) 题型:解答题
已知函数f(x)= (a、b为常数),且方程f(x)-x+12=0有两个实根为x1=3,x2=4.
(a、b为常数),且方程f(x)-x+12=0有两个实根为x1=3,x2=4.
(1)求函数f(x)的解析式;
(2)设k>1,解关于x的不等式f(x)<  .
.
查看答案和解析>>
科目:高中数学 来源:2015届辽宁盘锦市高一第一次阶段考试数学试卷(解析版) 题型:解答题
(12分)已知函数f(x)= (a,b为常数,且a≠0),满足f(2)=1,方程f(x)=x有唯一实数解,求函数f(x)的解析式和f[f(-4)]的值.
(a,b为常数,且a≠0),满足f(2)=1,方程f(x)=x有唯一实数解,求函数f(x)的解析式和f[f(-4)]的值.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年山东省莱芜市高三上学期10月测试理科数学 题型:解答题
(本小题满分l2分)
已知函数f(x)=a-
(1)求证:函数y=f(x)在(0,+∞)上是增函数;
(2)若f(x)<2x在(1,+∞)上恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年湖南省十二校高三第一次联考数学文卷 题型:解答题
( (本小题满分13分)
已知函数f(x)=(a-1)x+aln(x-2),(a<1).
(1)讨论函数f(x)的单调性;
(2)设a<0时,对任意x1、x2∈(2,+∞),<-4恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014届黑龙江省高一期末考试文科数学 题型:解答题
(12分)已知函数f(X)=㏒a(ax-1) (a>0且a≠1 )
)
(1)求函数的定义域 (2)讨论函数f(X)的单调性
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com