
如图,在平行四边形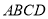 中,
中, ,
, ,将
,将 沿
沿 折起到
折起到 的位置.
的位置.
(1)求证: 平面
平面 ;
;
(2)当 取何值时,三棱锥
取何值时,三棱锥 的体积取最大值?并求此时三棱锥
的体积取最大值?并求此时三棱锥 的侧面积.
的侧面积.

(1)证明过程详见解析;(2) 时,三棱锥
时,三棱锥 体积取最大值,此时侧面积
体积取最大值,此时侧面积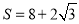 .
.
【解析】
试题分析:本题主要考查余弦定理、勾股定理、线面垂直、三角形面积公式、三棱锥的侧面积和体积等基础知识,考查学生的空间想象能力、逻辑推理能力.第一问,在 中,利用余弦定理得到BD的长,从而判断出
中,利用余弦定理得到BD的长,从而判断出 ,利用平行线,得
,利用平行线,得 ,
,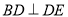 ,利用线面垂直的判定得
,利用线面垂直的判定得 平面
平面 ;
;
第二问,结合第一问的证明知,当 时,三棱锥的体积最大,此时
时,三棱锥的体积最大,此时 平面
平面 ,所以
,所以 和
和 为直角三角形,由线面垂直的判定可证出
为直角三角形,由线面垂直的判定可证出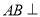 平面
平面 ,所以
,所以 ,所以
,所以 为直角三角形,所以三棱锥的侧面积为3个直角三角形之和.
为直角三角形,所以三棱锥的侧面积为3个直角三角形之和.
试题解析:(I)在 中,
中,

∵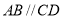 ∴
∴ ,
,
又
 ,
,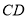 、
、
 平面
平面
∴ 平面
平面
(2)设E点到平面ABCD距离为 ,则
,则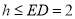 .
.
由(I)知
当 时,
时,
∵ ,
,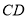 、
、
 平面
平面
∴ 平面
平面
∴当 时,
时,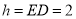 ,三棱锥
,三棱锥 的体积取最大值.
的体积取最大值.
此时 平面
平面 ,∴
,∴ 、
、
在 中,
中,

在Rt△ADE中,
∵ ,
, ,
, ,
, 、
、 平面
平面
∴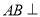 平面
平面 ∴
∴

综上, 时,三棱锥
时,三棱锥 体积取最大值,此时侧面积
体积取最大值,此时侧面积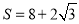 .
.
考点:余弦定理、勾股定理、线面垂直、三角形面积公式、三棱锥的侧面积和体积.


科目:高中数学 来源:2013-2014学年福建省福州市高三5月综合练习理科数学试卷(解析版) 题型:解答题
二阶矩阵A,B对应的变换对圆的区域作用结果如图所示.

(1)请写出一个满足条件的矩阵A,B;
(2)利用(1)的结果,计算C=BA,并求出曲线 在矩阵C对应的变换作用下的曲线方程.
在矩阵C对应的变换作用下的曲线方程.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省高考考前模拟理科数学试卷(解析版) 题型:选择题
已知曲线 :
: 和
和 :
: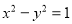 ,且曲线
,且曲线 的焦点分别为
的焦点分别为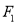 、
、 ,点
,点 是
是 和
和 的一个交点,则△
的一个交点,则△ 的形状是( )
的形状是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.都有可能
查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省高考考前模拟文科数学试卷(解析版) 题型:选择题
若命题 ,命题
,命题 ,那么( )
,那么( )
A.命题“ 或
或 ”为假 B.命题“
”为假 B.命题“ 且
且 ”为真
”为真
C.命题“ 或
或 ”为假 D.命题“
”为假 D.命题“ 且
且 ”为假
”为假
查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省厦门市高三5月适应性考试文科数学试卷(解析版) 题型:选择题
某市有大型超市200家、中型超市400家、小型超市1400家,为掌握各类超市的营业情况,现按分层抽样方法抽取一个容量为100的样本,应抽取中型超市( )
A. 70家 B.50家 C.20家 D.10家
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com