
如图,在三棱锥 中,平面
中,平面 平面
平面 ,
, 于点
于点 ,且
,且 ,
, ,
,
(1)求证:
(2)
(3)若 ,
, ,求三棱锥
,求三棱锥 的体积.
的体积.

(1)参考解析;(2)参考解析;(3)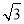
【解析】
试题分析:(1)由 ,
,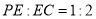 ,即可得到线段成比例,即得到直线平行,再根据直线与平面平行的判断定理即可得到结论.
,即可得到线段成比例,即得到直线平行,再根据直线与平面平行的判断定理即可得到结论.
(2)由平面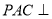 平面
平面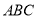 ,
,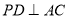 于点
于点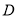 ,并且AC是平面PAC与平面ABC的交线,根据平面垂直的性质定理即可得PD垂直平面ABC,再根据平面与平面垂直的判断定理即可得到结论.
,并且AC是平面PAC与平面ABC的交线,根据平面垂直的性质定理即可得PD垂直平面ABC,再根据平面与平面垂直的判断定理即可得到结论.
(3)由 即可得AC=3.又由
即可得AC=3.又由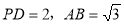 ,
,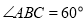 , 在三角形ABC中根据余弦定理即可求得BC的值.所以三角形ABC的面积可以求出来,由于PD垂直于平面ABC所以PD为三棱锥的高,即可求得结论.
, 在三角形ABC中根据余弦定理即可求得BC的值.所以三角形ABC的面积可以求出来,由于PD垂直于平面ABC所以PD为三棱锥的高,即可求得结论.
(1)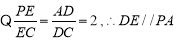 , 2分
, 2分
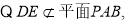
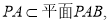
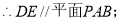 3分
3分
(2)因为平面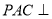 平面
平面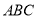 ,
,
且平面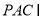 平面
平面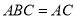 ,
,
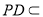 平面
平面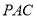 ,
,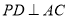 ,
,
所以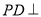 平面
平面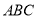 , 6分
, 6分
又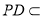 平面
平面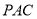 ,
,
所以平面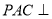 平面
平面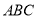 . 7分
. 7分
(3)由(2)可知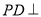 平面
平面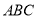 .
.
法一: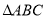 中,
中,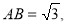
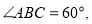
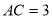 ,
,
由正弦定理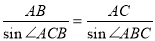 ,得
,得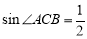 ,
,
因为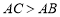 ,所以
,所以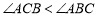 ,则
,则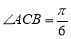 ,因此
,因此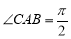 , 8分
, 8分
△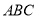 的面积
的面积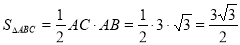 . 10分
. 10分
所以三棱锥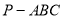 的体积
的体积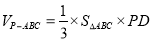
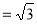 . 12分
. 12分
法二: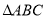 中,
中,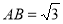 ,
,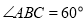
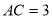 ,由余弦定理得:
,由余弦定理得:
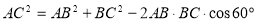 ,所以
,所以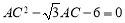 ,
,
所以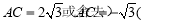 . 8分
. 8分
△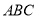 的面积
的面积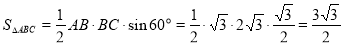 . 10分
. 10分
所以三棱锥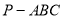 的体积
的体积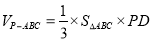
 . 12分
. 12分
考点:1.线面平行.2.面面垂直.3.三角形的余弦定理.4.三棱锥的体积.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2013-2014学年福建省漳州市毕业班质量检查理科数学试卷(解析版) 题型:选择题
执行如图所示的程序框图,如果输入 ,则输出的
,则输出的 的值为
的值为

A.7 B.9 C.2 D.13
查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省厦门市高三5月适应性考试文科数学试卷(解析版) 题型:选择题
“ ”是 “
”是 “ ”的( )
”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省三明市高三5月质量检查文科数学试卷(解析版) 题型:填空题
已知椭圆的焦点是双曲线的顶点,双曲线的焦点是椭圆的长轴顶点,若两曲线的离心率分别为 则
则 ______.
______.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年甘肃省武威市高三数学专题训练选择填空限时练四(解析版) 题型:选择题
要得到函数y=sin 的图象,只需将函数y=sin 2x的图象( )
的图象,只需将函数y=sin 2x的图象( )
A.向左平移 个单位
个单位
B.向右平移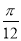 个单位
个单位
C.向左平移 个单位
个单位
D.向右平移 个单位
个单位
查看答案和解析>>
科目:高中数学 来源:2013-2014学年甘肃省武威市高三数学专题训练选择填空限时练二(解析版) 题型:选择题
设函数f(x)=x-2msin x+(2m-1)sin xcos x(m为实数)在(0,π)上为增函数,则m的取值范围为( )
A.[0, ] B.(0,
] B.(0, ) C.(0,
) C.(0, ] D.[0,
] D.[0,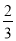 )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com