
25人排成5×5方阵,从中选出3人,要求其中任意2人既不同行也不同列,则不同的选法有( )
A.60种 B.100种
C.300种 D.600种
科目:高中数学 来源: 题型:
已知椭圆C过点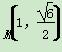 ,点F(-
,点F(-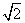 ,0)是椭圆的左焦点,点P,Q是椭圆C上的两个动点,且|PF|,|MF|,|QF|成等差数列.
,0)是椭圆的左焦点,点P,Q是椭圆C上的两个动点,且|PF|,|MF|,|QF|成等差数列.
(1)求椭圆C的标准方程;
(2)求证:线段PQ的垂直平分线经过一个定点A.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知某单位有50名职工,现在从中抽取10名职工,将全体职工随机按1~50编号,并按编号顺序平均分成10组,按各组内抽取的编号依次增加5进行系统抽样.
(1)若第5组抽出的号码为22,写出所有被抽出职工的号码;
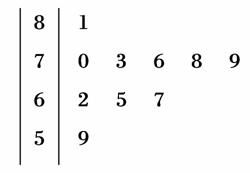
(2)分别统计这10名职工的体重(单位:kg),获得体重数据的茎叶图如图所示,求该样本的方差;
(3)在(2)的条件下,从这10名职工中随机抽取两名体重不轻于73 kg(≥73 kg)的职工,求体重为76 kg的职工被抽取到的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
为了调查某大学学生在某天上网的时间,随机对100名男生和100名女生进行了不记名的问卷调查.得到了如下的统计结果:
表1:男生上网时间与频数分布表
| 上网时间 (分钟) | [30,40) | [40,50) | [50,60) | [60,70) | [70,80] |
| 人数 | 5 | 25 | 30 | 25 | 15 |
表2:女生上网时间与频数分布表
| 上网时间 (分钟) | [30,40) | [40,50) | [50,60) | [60,70) | [70,80] |
| 人数 | 10 | 20 | 40 | 20 | 10 |
(1)从这100名男生中任意选出3人,求其中恰有1人上网时间少于60分钟的概率;
(2)完成下面的2×2列联表,并回答能否有90%的把握认为“大学生上网时间与性别有关”?
|
| 上网时间少 于60分钟 | 上网时间不少 于60分钟 | 合计 |
| 男生 | |||
| 女生 | |||
| 合计 |
附: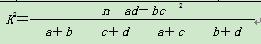
| P(K2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
按ABO血型系统学说,每个人的血型为A、B、O、AB型四种之一,依血型遗传学,当父母的血型中没有AB型时,子女的血型有可能是O型,若某人的血型是O型,则其父母血型的所有可能情况有( )
A.6种 B.9种
C.10种 D.12种
查看答案和解析>>
科目:高中数学 来源: 题型:
由数字1,2,3,4,
(1)可组成多少个三位数;
(2)可组成多少个没有重复数字的三位数;
(3)可组成多少个没有重复数字的三位数,且百位数字大于十位数字,十位数字大于个位数字.
查看答案和解析>>
科目:高中数学 来源: 题型:
10名同学合影,站成了前排3人,后排7人.现摄影师要从后排7人中抽2人站前排,其他人的相对顺序不变,则不同调整方法的种数为( )
A.C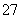 A
A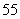 B.C
B.C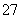 A
A
C.C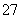 A
A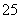 D.C
D.C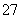 A
A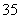
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com