
分析 根据角$(α+\frac{π}{3})$的终边经过点$P(2,\;4\sqrt{3})$,可得x=2,y=4$\sqrt{3}$,再根据tan$(α+\frac{π}{3})$=$\frac{y}{x}$,及两角和的正切函数公式计算求得结果.
解答 解:∵角$(α+\frac{π}{3})$的终边经过点$P(2,\;4\sqrt{3})$,
∴可得x=2,y=4$\sqrt{3}$,
∴tan$(α+\frac{π}{3})$=$\frac{y}{x}$=2$\sqrt{3}$=$\frac{tanα+\sqrt{3}}{1-\sqrt{3}tanα}$,
∴tanα=$\frac{{\sqrt{3}}}{7}$.
故答案为:$\frac{{\sqrt{3}}}{7}$.
点评 本题主要考查任意角的三角函数的定义,考查了两角和的正切函数公式的应用,属于基础题.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,-1,0} | B. | {-2,2,0} | C. | $\{2,-\frac{1}{2},\frac{{-5+\sqrt{41}}}{4}\}$ | D. | $\{2,\frac{1}{2},\frac{{-5-\sqrt{41}}}{4}\}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=$\sqrt{x^2}$,y=|x| | B. | y=$\frac{x^2}{x}$,y=x | ||
| C. | y=$\sqrt{x^2}$,$y={(\sqrt{x})^2}$ | D. | y=$\sqrt{x+1}•\sqrt{x-1}$,y=$\sqrt{{x^2}-1}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
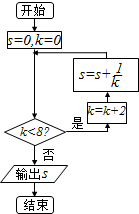
| A. | $\frac{25}{24}$ | B. | $\frac{11}{12}$ | C. | $\frac{5}{6}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com