
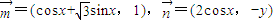 ,满足
,满足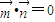 .
. ,且a=2,求△ABC面积的最大值.
,且a=2,求△ABC面积的最大值.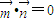 求得
求得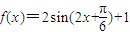 ,令
,令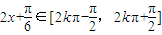 ,求得x的范围,即可求出f(x)的单调递增区间.
,求得x的范围,即可求出f(x)的单调递增区间.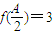 求得
求得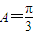 ,在△ABC中由余弦定理和基本不等式可得bc≤4,再由
,在△ABC中由余弦定理和基本不等式可得bc≤4,再由 求出它的最大值.
求出它的最大值. =
=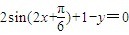 ,所以
,所以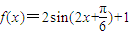 .…(3分)
.…(3分)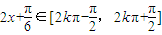 ,得
,得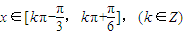 ,故f(x)的单调递增区间是
,故f(x)的单调递增区间是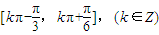 .…(6分)
.…(6分)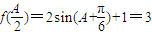 ,∴
,∴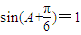 ,又
,又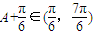 ,∴
,∴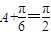 ,∴
,∴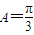 .…(8分)
.…(8分) ,
,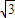 .…(12分)
.…(12分)

 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:高中数学 来源:中学教材全解 高中数学 必修1(人教A版) 人教A版 题型:044
某公司生产某种电子仪器的固定成本为20 000元,每生产一台仪器需增加投入100元,已知总收入满足函数:

(1)将利润表示为月产量的函数f(x);
(2)当月产量为何值时,公司所获利润最大?最大利润为多少元?
(总收益=总成本+利润)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
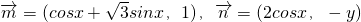 ,满足
,满足 .
.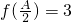 ,且a=2,求△ABC面积的最大值.
,且a=2,求△ABC面积的最大值.查看答案和解析>>
科目:高中数学 来源:2012-2013学年安徽省阜阳市颍上二中高三(上)期中数学试卷(文科)(解析版) 题型:解答题
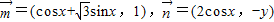 ,满足
,满足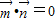 .
.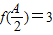 ,且a=2,求△ABC面积的最大值.
,且a=2,求△ABC面积的最大值.查看答案和解析>>
科目:高中数学 来源:2012年江西省宜春市高考数学模拟试卷(理科)(解析版) 题型:解答题
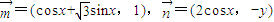 ,满足
,满足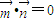 .
.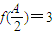 ,且a=2,求△ABC面积的最大值.
,且a=2,求△ABC面积的最大值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com