
【题目】如图1,在△ABC中, ![]() ,
, ![]() ,点D是BC的中点. ( I)求证:
,点D是BC的中点. ( I)求证: ![]() ;
;
( II)直线l过点D且垂直于BC,E为l上任意一点,求证: ![]() 为常数,并求该常数;
为常数,并求该常数;
( III)如图2,若 ![]() ,F为线段AD上的任意一点,求
,F为线段AD上的任意一点,求 ![]() 的范围.
的范围.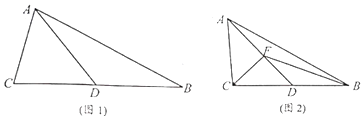
【答案】(I)证明:延长AD到A1使得AD=DA1 , 连接CA1 , A1B, ∵D是BC的中点,
∴四边形ACA1B是平行四边形,
∴ ![]() =
= ![]() +
+ ![]() ,
,
∵ ![]() ;
;
(II)证明:∵ ![]() =
= ![]() +
+ ![]() ,
,
∴ ![]() (
( ![]() ﹣
﹣ ![]() )=(
)=( ![]() +
+ ![]() )(
)( ![]() ﹣
﹣ ![]() )=
)= ![]()
![]() +
+ ![]()
![]() ,
,
∵DE⊥BC,∴ ![]()
![]() =0,
=0,
∵ ![]()
![]() =
= ![]() (
( ![]() )=
)= ![]() ,
,
∴ ![]()
![]() ﹣
﹣ ![]() )=
)= ![]()
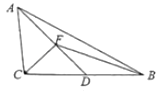
(III)解:△ABC中,| ![]() |=2,|
|=2,| ![]() |=1,cosA=
|=1,cosA= ![]() ,
, ![]() ,
,
∴| ![]() |=
|= ![]()
![]() =
= ![]() ,
,
同理 ![]() +
+ ![]() =2
=2 ![]() ,
,
∴ ![]() (
( ![]() +
+ ![]() )=
)= ![]() 2
2 ![]() =|
=| ![]() ||
|| ![]() |,
|,
设| ![]() |=x,则|
|=x,则| ![]() |=
|= ![]() ﹣x(0
﹣x(0 ![]() ),
),
∴ ![]() (
( ![]() +
+ ![]() )=2x(
)=2x( ![]() ﹣x)≤2
﹣x)≤2 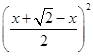 =1,当且仅当x=
=1,当且仅当x= ![]() 时取等号,
时取等号,
∴ ![]() (
( ![]() +
+ ![]() )∈(0,1].
)∈(0,1].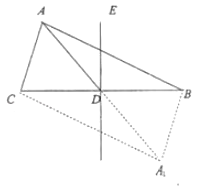
【解析】( I)延长AD到A1使得AD=DA1 , 连接CA1 , A1B,证明四边形ACA1B是平行四边形,即可证明: ![]() ;( II)证明
;( II)证明 ![]() (
( ![]() ﹣
﹣ ![]() )=(
)=( ![]() +
+ ![]() )(
)( ![]() ﹣
﹣ ![]() )=
)= ![]()
![]() +
+ ![]()
![]() ,即可得出:
,即可得出: ![]() 为常数,并求该常数;(III)确定
为常数,并求该常数;(III)确定 ![]() (
( ![]() +
+ ![]() )=2x(
)=2x( ![]() ﹣x),利用基本不等式,求
﹣x),利用基本不等式,求 ![]() 的范围.
的范围.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某校从参加高一年级期中考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[40,50),[50,60)…[90,100]后得到如下部分频率分布直方图.观察图形的信息,回答下列问题: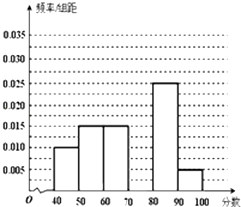
(1)求分数在[70,80)内的频率,并补全这个频率分布直方图;
(2)用分层抽样的方法在分数段为[60,80)的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任取2人,求至多有1人在分数段[70,80)的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在多面体SP﹣ABCD中,底面ABCD为矩形,AB=PC=1,AD=AS=2,且AS∥CP且AS⊥面ABCD,E为BC的中点.
(1)求证:AE∥面SPD;
(2)求三棱锥S-BPD的体积。

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=loga(x+1),g(x)=loga(4﹣2x),a>0且a≠1.
(1)求函数y=f(x)﹣g(x)的定义域;
(2)求使不等式f(x)>g(x)成立的实数x的取值范围;
(3)求函数y=2f(x)﹣g(x)﹣f(1)的零点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在矩形ABCD中,对角线AC与相邻两边所成的角为α,β,则cos2α+cos2β=1.类比到空间中一个正确命题是:在长方体ABCD﹣A1B1C1D1中,对角线AC1与相邻三个面所成的角为α,β,γ,则有 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知全集U=R,集合A={x|1<x<4},B={x|x≤3m﹣4或x≥8+m}(m<6)
(1)若m=2,求A∩(UB)
(2)若A∩(UB)=,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等比数列![]() 中,
中, ![]() 分别是下表中第
分别是下表中第![]() 行中的某一个数,且
行中的某一个数,且![]() 中任何两个数不在下表的同一列中.
中任何两个数不在下表的同一列中.
第 | 第 | 第 | |
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
(1)求数列![]() 的通项公式;
的通项公式;
(2)设![]() ,求数列
,求数列![]() 的前
的前![]() 项和.
项和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com