
 ,sin(α+β)=
,sin(α+β)= ,α与β均为锐角,求cos
,α与β均为锐角,求cos .(cos
.(cos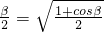 )
) ,∴cosα=
,∴cosα=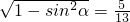 .…(2分)
.…(2分) ,0<β<
,0<β< ,
, ,∵sin(α+β)<sinα,∴α+β<α不可能.
,∵sin(α+β)<sinα,∴α+β<α不可能. <α+β<π.
<α+β<π. .…(6分)
.…(6分) •
• •
•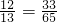 ,…(10分)
,…(10分) ,
, <
< .
.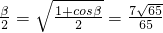 .…(13分)
.…(13分)

科目:高中数学 来源: 题型:
| α |
| 2 |
| α |
| 2 |
| π |
| 4 |
| 6sinα+cosα |
| 3sinα-2cosα |
| cos2α | ||||
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| b |
| π |
| 2 |
| π |
| 2 |
| a |
| b |
| 2 |
| π |
| 4 |
| a |
| b |
查看答案和解析>>
科目:高中数学 来源: 题型:
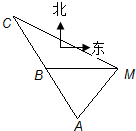 (2009•台州二模)如图,已知A、B、C是一条直路上的三点,一个人从A出发行走到B处时,望见塔M(将塔M视为与A、B、C在同一水平面上一点)在正东方向且A在东偏南α方向,继续行走1km在到达C处时,望见塔M在东偏南β方向,则塔M到直路ABC的最短距离为( )
(2009•台州二模)如图,已知A、B、C是一条直路上的三点,一个人从A出发行走到B处时,望见塔M(将塔M视为与A、B、C在同一水平面上一点)在正东方向且A在东偏南α方向,继续行走1km在到达C处时,望见塔M在东偏南β方向,则塔M到直路ABC的最短距离为( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com