
分析 (1)由函数f(x)=$\sqrt{2}$sin(2x-$\frac{π}{4}$)+1,可得周期T=$\frac{2π}{2}$.当sin(2x-$\frac{π}{4}$)=1时,解得x,进而得到函数f(x)的最大值.由$sin(2x-\frac{π}{4})$=0,解得x,可得函数f(x)的对称中心.
(2)利用几何画板可得图象.
解答 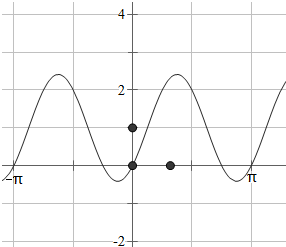 解:(1)∵函数f(x)=$\sqrt{2}$sin(2x-$\frac{π}{4}$)+1,可得周期T=$\frac{2π}{2}$=π.
解:(1)∵函数f(x)=$\sqrt{2}$sin(2x-$\frac{π}{4}$)+1,可得周期T=$\frac{2π}{2}$=π.
当sin(2x-$\frac{π}{4}$)=1时,即$2x-\frac{π}{4}$=2kπ+$\frac{π}{2}$,解得x=kπ+$\frac{3π}{8}$(k∈Z),函数f(x)取得最大值$\sqrt{2}$+1.
由$sin(2x-\frac{π}{4})$=0,可得$2x-\frac{π}{4}$=kπ,解得x=$\frac{kπ}{2}$+$\frac{π}{8}$,(k∈Z),可得函数f(x)的对称中心$(\frac{kπ}{2}+\frac{π}{8},0)$.
(2)利用几何画板可得:y=f(x)在[-$\frac{π}{2}$,$\frac{π}{2}$]上的图象.
点评 本题考查了三角函数的图象与性质、几何画板的应用,考查了推理能力与计算能力,属于中档题.


 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
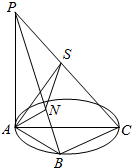 如图,AC为圆O的直径,B为圆周上不与点A、C重合的点,PA垂直于圆O所在的平面,连结PB、PC、AB、BC,作AN⊥PB,AS⊥PC,连结SN,则图中直角三角形个数为( )
如图,AC为圆O的直径,B为圆周上不与点A、C重合的点,PA垂直于圆O所在的平面,连结PB、PC、AB、BC,作AN⊥PB,AS⊥PC,连结SN,则图中直角三角形个数为( )| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{8}$ | B. | $\frac{4-π}{4}$ | C. | $\frac{4-π}{8}$ | D. | $\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 过定点(4p,0) | B. | 过定点(2p,0) | C. | 过定点(p,0) | D. | 过抛物线焦点 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com