
△ABC的三个内角A、B、C成等差数列,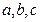 分别为三个内角A、B、C所对的边,
分别为三个内角A、B、C所对的边,
求证: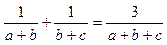 。 (13分)
。 (13分)
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源: 题型:解答题
如图,正在海上A处执行任务的渔政船甲和在B处执行任务的渔政船乙,同时收到同一片海域上一艘渔船丙的求救信号,此时渔船丙在渔政船甲的南偏东40°方向距渔政船甲70km的C处,渔政船乙在渔政船甲的南偏西20°方向的B处,两艘渔政船协调后立即让渔政船甲向渔船丙所在的位置C处沿直线AC航行前去救援,渔政船乙仍留在B处执行任务,渔政船甲航行30km到达D处时,收到新的指令另有重要任务必须执行,于是立即通知在B处执行任务的渔政船乙前去救援渔船丙(渔政船乙沿直线BC航行前去救援渔船丙),此时B、D两处相距42km,问渔政船乙要航行多少距离才能到达渔船丙所在的位置C处实施营救.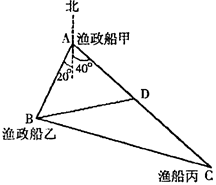
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
三、解答题(本大题有5道小题,各小题12分,共60分)
17.在 中,
中, 分别是角
分别是角 的对边,向量
的对边,向量 ,
,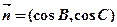 ,且
,且 .
.
(1)求角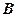 的大小;
的大小;
(2)设 ,且
,且 的最小正周期为
的最小正周期为 ,求
,求 在
在
区间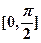 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
已知函数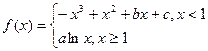
 的图象过坐标原点O,且在点
的图象过坐标原点O,且在点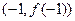 处的切线的斜率是
处的切线的斜率是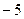 .
.
(Ⅰ)求实数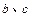 的值;
的值;
(Ⅱ)求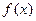 在区间
在区间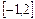 上的最大值;
上的最大值;
(Ⅲ)对任意给定的正实数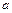 ,曲线
,曲线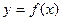 上是否存在两点P、Q,使得
上是否存在两点P、Q,使得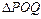 是以O为直角顶点的直角三角形,且此三角形斜边中点在
是以O为直角顶点的直角三角形,且此三角形斜边中点在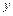 轴上?说明理由。
轴上?说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
港口A北偏东30°方向的C处有一检查站,港口正东方向的B处有一轮船,距离检查站为31海里,该轮船从B处沿正西方向航行20海里后到达D处观测站,已知观测站与检查站距离21海里,问此时轮船离港口A还有多远?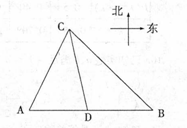
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com