
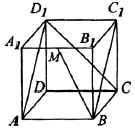
 ��ͼ��������ABCD-A1B1C1D1���ⳤΪ1��M��A1B1���е㣬�������ĸ����⣺
��ͼ��������ABCD-A1B1C1D1���ⳤΪ1��M��A1B1���е㣬�������ĸ����⣺���� ��������������������ο����֤��ÿһ��ѡ�M����ABC1D1�ľ������B1����ABC1D1�ľ���$\frac{1}{2}$B1C��BC����ABC1D1���ɵĽǼ�Ϊ��CBC1=45�㣬���ĸ����ϵ�ͶӰ��Ϊ�����λ�Ϊ�����Σ���СΪ�����Σ�BE��CD1���ɵĽǼ�ΪBE��BA1���ɵĽǣ�
��� �⣺������ABCD-A1B1C1D1���ⳤΪ1��M��A1B1���е㣬
���ڢ٣�BC����ABC1D1���ɵĽǼ�Ϊ��CBC1=45�㣬����ȷ��
���ڢڣ����ĸ����ϵ�ͶӰ��Ϊ�����λ�Ϊ�����Σ���СΪ�����Σ����Ϊ$\frac{1}{2}$������ȷ��
���ڢۣ�M��A1B1��A1B1����ABC1D1����M����ABC1D1�ľ������B1����ABC1D1�ľ���$\frac{1}{2}$B1C=$\frac{\sqrt{2}}{2}$����ԣ�
���ڢܣ�BM��CD1���ɵĽǼ�ΪBM��BA1���ɵĽǣ�����A1BM��A1M=$\frac{1}{2}$��A1B=2��BM=$\frac{\sqrt{5}}{2}$��
�����Ҷ����ɵ�cos��A1BE=$\frac{3\sqrt{10}}{10}$����sin��A1BM=$\frac{\sqrt{10}}{10}$��BM��CD1���ɵĽ�Ϊ$arcsin\frac{{\sqrt{10}}}{10}$������ȷ��
�ʴ�Ϊ���٢ڢܣ�
���� ���⿼�����������жϣ��ǻ����⣬����ʱҪ�������⣬ע��ռ�˼ά������������


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2}$ | B�� | -$\frac{1}{2}$ | C�� | 1 | D�� | -1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y=x3 | B�� | y=lgx | C�� | y=|x| | D�� | y=x-1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com