
【题目】在平面直角坐标系![]() 中,动点
中,动点![]() 在抛物线
在抛物线![]() 上运动,点
上运动,点![]() 在
在![]() 轴上的射影为
轴上的射影为![]() ,动点
,动点![]() 满足
满足![]() .
.
![]() 求动点
求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
![]() 过点
过点![]() 作互相垂直的直线
作互相垂直的直线![]() ,
,![]() ,分别交曲线
,分别交曲线![]() 于点
于点![]() ,
,![]() 和
和![]() ,
,![]() ,记
,记![]() ,
,![]() 的面积分别为
的面积分别为![]() ,
,![]() ,问:
,问:![]() 是否为定值?若为定值,求出该定值;若不为定值,请说明理由.
是否为定值?若为定值,求出该定值;若不为定值,请说明理由.
 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,右顶点为
,右顶点为![]() ,且离心率为
,且离心率为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)互相平行的两条直线![]() 分别过
分别过![]() ,且直线
,且直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,直线
两点,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,若四边形
两点,若四边形![]() 的面积为
的面积为![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某服装店对过去100天其实体店和网店的销售量(单位:件)进行了统计,制成频率分布直方图如下:
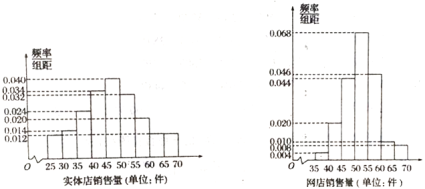
(1)若将上述频率视为概率,已知该服装店过去100天的销售中,实体店和网店销售量都不低于50件的概率为0.4,求过去100天的销售中,实体店和网店至少有一边销售量不低于50件的天数;
(2)若将上述频率视为概率,已知该服装店实体店每天的人工成本为500元,门市成本为1200元,每售出一件利润为50元,求该门市一天获利不低于800元的概率;
(3)根据销售量的频率分布直方图,求该服装店网店销售量中位数的估计值(精确到0.01).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在心理学研究中,常采用对比试验的方法评价不同心理暗示对人的影响,具体方法如下:将参加试验的志愿者随机分成两组,一组接受甲种心理暗示,另一组接受乙种心理暗示,通过对比这两组志愿者接受心理暗示后的结果来评价两种心理暗示的作用.现有6名男志愿者A1,A2,A3,A4,A5,A6和4名女志愿者B1,B2,B3,B4,从中随机抽取5人接受甲种心理暗示,另5人接受乙种心理暗示.
(1)求接受甲种心理暗示的志愿者中包含A1但不包含B1的概率;
(2)用X表示接受乙种心理暗示的女志愿者人数,求X的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且点
,且点![]()
![]() 在函数
在函数![]() 的图像上;
的图像上;
(1)求数列![]() 的通项公式;
的通项公式;
(2)设数列![]() 满足:
满足:![]() ,
,![]() ,求
,求![]() 的通项公式;
的通项公式;
(3)在第(2)问的条件下,若对于任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有三张形状、大小、质地完全一致的卡片,在每张卡片上写上0,1,2,现从中任意抽取一张,将其上数字记作x,然后放回,再抽取一张,其上数字记作y,令![]() .求:
.求:
(1)![]() 所取各值的分布列;
所取各值的分布列;
(2)随机变量![]() 的数学期望与方差.
的数学期望与方差.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com