
【题目】![]() 有最大值,且最大值大于
有最大值,且最大值大于![]() .
.
(1)求![]() 的取值范围;
的取值范围;
(2)当![]() 时,
时,![]() 有两个零点
有两个零点![]() ,证明:
,证明:![]() .
.
(参考数据:![]() )
)
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)求出函数![]() 的定义域为
的定义域为![]() ,
,![]() ,分
,分![]() 和
和![]() 两种情况讨论,分析函数
两种情况讨论,分析函数![]() 的单调性,求出函数
的单调性,求出函数![]() 的最大值,即可得出关于实数
的最大值,即可得出关于实数![]() 的不等式,进而可求得实数
的不等式,进而可求得实数![]() 的取值范围;
的取值范围;
(2)利用导数分析出函数![]() 在
在![]() 上递增,在
上递增,在![]() 上递减,可得出
上递减,可得出![]() ,由
,由 ,构造函数
,构造函数![]() ,证明出
,证明出![]() ,进而得出
,进而得出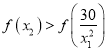 ,再由函数
,再由函数![]() 在区间
在区间![]() 上的单调性可证得结论.
上的单调性可证得结论.
(1)函数![]() 的定义域为
的定义域为![]() ,且
,且![]() .
.
当![]() 时,对任意的
时,对任意的![]() ,
,![]() ,
,
此时函数![]() 在
在![]() 上为增函数,函数
上为增函数,函数![]() 为最大值;
为最大值;
当![]() 时,令
时,令![]() ,得
,得![]() .
.
当![]() 时,
时,![]() ,此时函数
,此时函数![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,此时函数
,此时函数![]() 单调递减.
单调递减.
所以,函数![]() 在
在![]() 处取得极大值,亦即最大值,
处取得极大值,亦即最大值,
即![]() ,解得
,解得![]() .
.
综上所述,实数![]() 的取值范围是
的取值范围是![]() ;
;
(2)当![]() 时,
时,![]() ,定义域为
,定义域为![]() ,
,
![]() ,当
,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
所以,函数![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .
.
由于函数![]() 有两个零点
有两个零点![]() 、
、![]() 且
且![]() ,
,![]() ,
,
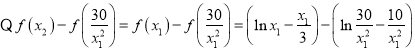
![]() ,
,
构造函数![]() ,其中
,其中![]() ,
,
![]() ,
,
令![]() ,
,![]() ,当
,当![]() 时,
时,![]() ,
,
所以,函数![]() 在区间
在区间![]() 上单调递减,则
上单调递减,则![]() ,则
,则![]() .
.
所以,函数![]() 在区间
在区间![]() 上单调递减,
上单调递减,
![]() ,
,![]() ,
,
即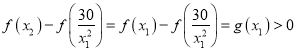 ,即
,即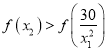 ,
,
![]() ,
,![]() 且
且![]() ,而函数
,而函数![]() 在
在![]() 上为减函数,
上为减函数,
所以,![]() ,因此,
,因此,![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,动点
中,动点![]() 在抛物线
在抛物线![]() 上运动,点
上运动,点![]() 在
在![]() 轴上的射影为
轴上的射影为![]() ,动点
,动点![]() 满足
满足![]() .
.
![]() 求动点
求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
![]() 过点
过点![]() 作互相垂直的直线
作互相垂直的直线![]() ,
,![]() ,分别交曲线
,分别交曲线![]() 于点
于点![]() ,
,![]() 和
和![]() ,
,![]() ,记
,记![]() ,
,![]() 的面积分别为
的面积分别为![]() ,
,![]() ,问:
,问:![]() 是否为定值?若为定值,求出该定值;若不为定值,请说明理由.
是否为定值?若为定值,求出该定值;若不为定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为担任班主任的教师办理手机语音月卡套餐,为了解通话时长,采用随机抽样的方法,得到该校100位班主任每人的月平均通话时长![]() (单位:分钟)的数据,其频率分布直方图如图所示,将频率视为概率.
(单位:分钟)的数据,其频率分布直方图如图所示,将频率视为概率.
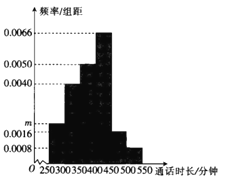
(1)求图中![]() 的值;
的值;
(2)估计该校担任班主任的教师月平均通话时长的中位数;
(3)在![]() ,
,![]() 这两组中采用分层抽样的方法抽取6人,再从这6人中随机抽取2人,求抽取的2人恰在同一组的概率.
这两组中采用分层抽样的方法抽取6人,再从这6人中随机抽取2人,求抽取的2人恰在同一组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
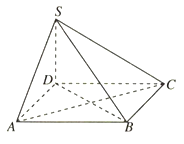
【题目】如图所示,四棱锥![]() 的底面为正方形,
的底面为正方形,![]() 底面
底面![]() ,则下列结论中正确结论的序号是_________________.
,则下列结论中正确结论的序号是_________________.
①![]() ;②
;②![]() 平面
平面![]() ;③
;③![]() 与平面
与平面![]() 所成的角等于
所成的角等于![]() 与平面
与平面![]() 所成的角;④
所成的角;④![]() 与
与![]() 所成的角等于
所成的角等于![]() 与
与![]() 所成的角.
所成的角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆的中心在原点,其左焦点![]() 与抛物线
与抛物线![]() 的焦点重合,过
的焦点重合,过![]() 的直线
的直线![]() 与椭圆交于
与椭圆交于![]() 、
、![]() 两点,与抛物线交于
两点,与抛物线交于![]() 、
、![]() 两点.当直线
两点.当直线![]() 与
与![]() 轴垂直时,
轴垂直时,![]() .
.
(1)求椭圆的方程;
(2)求![]() 的最大值和最小值.
的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设![]() 是椭圆
是椭圆![]() 的左焦点,直线:
的左焦点,直线:![]() 与
与![]() 轴交于
轴交于![]() 点,
点,![]() 为椭圆的长轴,已知
为椭圆的长轴,已知![]() ,且
,且![]() ,过
,过![]() 点作斜率为
点作斜率为![]() 直线
直线![]() 与椭圆相交于不同的两点
与椭圆相交于不同的两点![]() ,
,
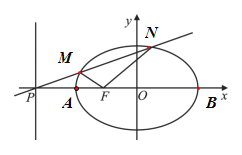
(1)当![]() 时,线段
时,线段![]() 的中点为
的中点为![]() ,过
,过![]() 作
作![]() 交
交![]() 轴于点
轴于点![]() ,求
,求![]() ;
;
(2)求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,曲线![]() (
(![]() 为参数),在以原点
为参数),在以原点![]() 为极点,
为极点,![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() .
.
(1)写出![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 在曲线
在曲线![]() 上,点
上,点![]() 在曲线
在曲线![]() 上,求
上,求![]() 的最小值及此时点
的最小值及此时点![]() 的直角坐标.
的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年底,湖北省武汉市等多个地区陆续出现感染新型冠状病毒肺炎的患者.为及时有效地对疫情数据进行流行病学统计分析,某地研究机构针对该地实际情况,根据该地患者是否有武汉旅行史与是否有确诊病例接触史,将新冠肺炎患者分为四类:有武汉旅行史(无接触史),无武汉旅行史(无接触史),有武汉旅行史(有接触史)和无武汉旅行史(有接触史),统计得到以下相关数据.
(1)请将列联表填写完整:
有接触史 | 无接触史 | 总计 | |
有武汉旅行史 | 27 | ||
无武汉旅行史 | 18 | ||
总计 | 27 | 54 |
(2)能否在犯错误的概率不超过0.025的前提下认为有武汉旅行史与有确诊病例接触史有关系?
附:![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com