
【题目】椭圆的中心在原点,其左焦点![]() 与抛物线
与抛物线![]() 的焦点重合,过
的焦点重合,过![]() 的直线
的直线![]() 与椭圆交于
与椭圆交于![]() 、
、![]() 两点,与抛物线交于
两点,与抛物线交于![]() 、
、![]() 两点.当直线
两点.当直线![]() 与
与![]() 轴垂直时,
轴垂直时,![]() .
.
(1)求椭圆的方程;
(2)求![]() 的最大值和最小值.
的最大值和最小值.
【答案】(1)![]() (2)最大值
(2)最大值![]() ;最小值
;最小值![]()
【解析】
(1)由抛物线方程,得焦点![]() ,联立抛物线方程与直线
,联立抛物线方程与直线![]() 的方程,得出
的方程,得出![]() ,根据对称性以及
,根据对称性以及![]() ,得出
,得出![]() ,从而得出
,从而得出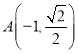 ,代入椭圆方程,根据椭圆的性质得出椭圆的方程;
,代入椭圆方程,根据椭圆的性质得出椭圆的方程;
(2)讨论直线![]() 与
与![]() 轴是否垂直,当直线
轴是否垂直,当直线![]() 与
与![]() 轴不垂直时,设出直线
轴不垂直时,设出直线![]() 方程,并与椭圆联立,利用韦达定理以及向量的数量积公式,化简得出
方程,并与椭圆联立,利用韦达定理以及向量的数量积公式,化简得出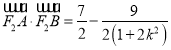 ,再求最值,即可得出结论.
,再求最值,即可得出结论.
解:(1)由抛物线方程,得焦点![]() .
.
设椭圆的方程:![]() .
.
解方程组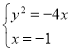 得
得![]() .
.
由于抛物线、椭圆都关于![]() 轴对称,
轴对称,
∴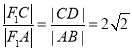 ,
,![]() ,∴
,∴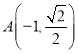 .
.
∴![]() 又
又![]() ,
,
因此,![]() ,解得
,解得![]() ,并推得
,并推得![]() .
.
故椭圆的方程为![]() .
.
(2)由(1)知,![]()
①若![]() 垂直于
垂直于![]() 轴,则
轴,则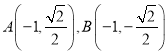 ,
,
∴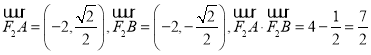
②若![]() 与
与![]() 轴不垂直,设直线
轴不垂直,设直线![]() 的斜率为
的斜率为![]() ,则直线
,则直线![]() 的方程为
的方程为![]()
由![]() 得
得![]()
∵![]() ,∴方程有两个不等的实数根.
,∴方程有两个不等的实数根.
设![]() .
.
![]()
∴![]()
![]()
![]()

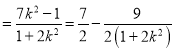
![]() ,则
,则![]()
综上,![]()
所以当直线![]() 垂于
垂于![]() 轴时,
轴时,![]() 取得最大值
取得最大值![]()
当直线![]() 与
与![]() 轴重合时,
轴重合时,![]() 取得最小值
取得最小值![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】在心理学研究中,常采用对比试验的方法评价不同心理暗示对人的影响,具体方法如下:将参加试验的志愿者随机分成两组,一组接受甲种心理暗示,另一组接受乙种心理暗示,通过对比这两组志愿者接受心理暗示后的结果来评价两种心理暗示的作用.现有6名男志愿者A1,A2,A3,A4,A5,A6和4名女志愿者B1,B2,B3,B4,从中随机抽取5人接受甲种心理暗示,另5人接受乙种心理暗示.
(1)求接受甲种心理暗示的志愿者中包含A1但不包含B1的概率;
(2)用X表示接受乙种心理暗示的女志愿者人数,求X的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知直线
中,已知直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() ,直线
,直线![]() 与曲线
与曲线![]() 的交点为
的交点为![]() 、
、![]() ,求
,求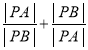 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国著名数学家陈景润在哥德巴赫猜想的研究中取得了世界瞩目的成就,哥德巴赫猜想内容是“每个大于![]() 的偶数可以表示为两个素数的和”( 注:如果一个大于
的偶数可以表示为两个素数的和”( 注:如果一个大于![]() 的整数除了
的整数除了![]() 和自身外无其他正因数,则称这个整数为素数),在不超过
和自身外无其他正因数,则称这个整数为素数),在不超过![]() 的素数中,随机选取
的素数中,随机选取![]() 个不同的素数
个不同的素数![]() 、
、![]() ,则
,则![]() 的概率是( )
的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】炼钢是一个氧化降碳的过程,由于钢水含碳量的多少直接影响冶炼时间的长短,因此必须掌握钢水含碳量和冶炼时间的关系.现已测得炉料熔化完毕时钢水的含碳量![]() 与冶炼时间
与冶炼时间![]() (从炉料熔化完毕到出钢的时间)的一组数据,如下表所示:
(从炉料熔化完毕到出钢的时间)的一组数据,如下表所示:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 104 | 180 | 190 | 177 | 147 | 134 | 150 | 191 | 204 | 121 |
| 100 | 200 | 210 | 185 | 155 | 135 | 170 | 205 | 235 | 125 |
| 10400 | 36000 | 39900 | 32745 | 22785 | 18090 | 25500 | 39155 | 47940 | 15125 |
(1)据统计表明,![]() 与
与![]() 之间具有线性相关关系,请用相关系数
之间具有线性相关关系,请用相关系数![]() 加以说明(
加以说明(![]()
![]() ,则认为
,则认为![]() 与
与![]() 有较强的线性相关关系,否则认为没有较强的线性相关关系,
有较强的线性相关关系,否则认为没有较强的线性相关关系,![]() 精确到0.001);
精确到0.001);
(2)建立![]() 关于
关于![]() 的回归方程(回归系数的结果精确到0.01);
的回归方程(回归系数的结果精确到0.01);
(3)根据(2)中的结论,预测钢水含碳量为160个0.01%的冶炼时间.
参考公式:回归方程![]() 中斜率和截距的最小二乘估计分别为
中斜率和截距的最小二乘估计分别为 ,
,
![]() ,相关系数
,相关系数
参考数据: ,
,
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】4月23日是“世界读书日”,某中学开展了一系列的读书教育活动.学校为了解高三学生课外阅读情况,采用分层抽样的方法从高三某班甲、乙、丙、丁四个读书小组(每名学生只能参加一个读书小组)学生抽取12名学生参加问卷调查.各组人数统计如下:
小组 | 甲 | 乙 | 丙 | 丁 |
人数 | 12 | 9 | 6 | 9 |
(1)从参加问卷调查的12名学生中随机抽取2人,求这2人来自同一个小组的概率;
(2)从已抽取的甲、丙两个小组的学生中随机抽取2人,用![]() 表示抽得甲组学生的人数,求随机变量
表示抽得甲组学生的人数,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com