练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】我国著名数学家陈景润在哥德巴赫猜想的研究中取得了世界瞩目的成就，哥德巴赫猜想内容是“每个大于的偶数可以表示为两个素数的和”（ 注：如果一个大于的整数除了和自身外无其他正因数，则称这个整数为素数），在不超过的素数中，随机选取个不同的素数、，则的概率是（ ）

    A.B.C.D.

    【答案】B

    【解析】

    先列举出不超过的素数，并列举出所有的基本事件以及事件“在不超过的素数中，随机选取个不同的素数、，满足”所包含的基本事件，利用古典概型的概率公式可求得所求事件的概率.

    不超过的素数有：、、、、、，

    在不超过的素数中，随机选取个不同的素数，所有的基本事件有：、、、、、、、、、、、、、、，共种情况，

    其中，事件“在不超过的素数中，随机选取个不同的素数、，且”包含的基本事件有：、、、，共种情况，

    因此，所求事件的概率为.

    故选：B.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，四棱锥中，平面底面ABCD，是等边三角形，底面ABCD为梯形，且，，．

    Ⅰ证明：；

    Ⅱ求A到平面PBD的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】四棱锥中，平面，底面为菱形，且有，，是线段上一点，且与所成角的正弦值是.

    （1）求的大小；

    （2）若与平面所成的角的正弦值是，求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知动圆经过定点，且与定直线相切．

    （1）求动圆圆心的轨迹方程；

    （2）已知点，过点作直线与交于，两点，过点作轴的垂线分别与直线，交于点，（为原点），求证：为线段中点．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某学校为担任班主任的教师办理手机语音月卡套餐，为了解通话时长，采用随机抽样的方法，得到该校100位班主任每人的月平均通话时长（单位：分钟）的数据，其频率分布直方图如图所示，将频率视为概率.

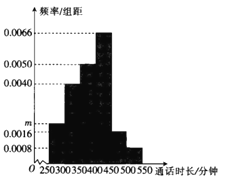
    （1）求图中的值；

    （2）估计该校担任班主任的教师月平均通话时长的中位数；

    （3）在，这两组中采用分层抽样的方法抽取6人，再从这6人中随机抽取2人，求抽取的2人恰在同一组的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆，上、下顶点分别是、，上、下焦点分别是、，焦距为，点在椭圆上.

    （1）求椭圆的方程；

    （2）若为椭圆上异于、的动点，过作与轴平行的直线，直线与交于点，直线与直线交于点，判断是否为定值，说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】椭圆的中心在原点，其左焦点与抛物线的焦点重合，过的直线与椭圆交于、两点，与抛物线交于、两点．当直线与轴垂直时，．

    （1）求椭圆的方程；

    （2）求的最大值和最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设复数β=x+yi（x，y∈R）与复平面上点P（x，y）对应．

    （1）若β是关于t的一元二次方程t2﹣2t+m=0（m∈R）的一个虚根，且|β|=2，求实数m的值；

    （2）设复数β满足条件|β+3|+（﹣1）n|β﹣3|=3a+（﹣1）na（其中n∈N*、常数），当n为奇数时，动点P（x、y）的轨迹为C1．当n为偶数时，动点P（x、y）的轨迹为C2．且两条曲线都经过点，求轨迹C1与C2的方程；

    （3）在（2）的条件下，轨迹C2上存在点A，使点A与点B（x0，0）（x0＞0）的最小距离不小于，求实数x0的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知定义在R上的函数满足，且为偶函数，若在内单调递减，则下面结论正确的是（ ）

    A. B.

    C. D.

    查看答案和解析>>

    同步练习册答案