【题目】炼钢是一个氧化降碳的过程，由于钢水含碳量的多少直接影响冶炼时间的长短，因此必须掌握钢水含碳量和冶炼时间的关系.现已测得炉料熔化完毕时钢水的含碳量
与冶炼时间
（从炉料熔化完毕到出钢的时间）的一组数据，如下表所示：
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 104 | 180 | 190 | 177 | 147 | 134 | 150 | 191 | 204 | 121 |
| 100 | 200 | 210 | 185 | 155 | 135 | 170 | 205 | 235 | 125 |
| 10400 | 36000 | 39900 | 32745 | 22785 | 18090 | 25500 | 39155 | 47940 | 15125 |
（1）据统计表明，与之间具有线性相关关系，请用相关系数
加以说明（
，则认为与有较强的线性相关关系，否则认为没有较强的线性相关关系，精确到0.001）；
（2）建立关于的回归方程（回归系数的结果精确到0.01）；
（3）根据（2）中的结论，预测钢水含碳量为160个0.01%的冶炼时间.
参考公式：回归方程
中斜率和截距的最小二乘估计分别为
，
，相关系数
参考数据：
，
.
科目：高中数学 来源： 题型：
【题目】已知动圆C过定点F（2，0），且与直线x=-2相切，圆心C的轨迹为E，
（1）求圆心C的轨迹E的方程；
（2）若直线l交E与P，Q两点，且线段PQ的中心点坐标（1，1），求|PQ|．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知动圆经过定点
，且与定直线
相切．
（1）求动圆圆心
的轨迹方程
；
（2）已知点
，过点
作直线
与交于
，
两点，过点作
轴的垂线分别与直线
，
交于点
，
（
为原点），求证：为线段
中点．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
，上、下顶点分别是
、
，上、下焦点分别是
、
，焦距为
，点
在椭圆上.
（1）求椭圆的方程；
（2）若
为椭圆上异于、的动点，过作与
轴平行的直线
，直线
与交于点
，直线
与直线
交于点
，判断
是否为定值，说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】椭圆的中心在原点，其左焦点
与抛物线
的焦点重合，过的直线
与椭圆交于
、
两点，与抛物线交于
、
两点．当直线与
轴垂直时，
．
（1）求椭圆的方程；
（2）求
的最大值和最小值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】从数列
中取出部分项组成的数列称为数列的“子数列”.
（1）若等差数列的公差
，其子数列
恰为等比数列，其中
，
，
，求
；
（2）若
，
，判断数列
是否为的“子数列”，并证明你的结论.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设复数β=x+yi（x，y∈R）与复平面上点P（x，y）对应．
（1）若β是关于t的一元二次方程t2﹣2t+m=0（m∈R）的一个虚根，且|β|=2，求实数m的值；
（2）设复数β满足条件|β+3|+（﹣1）n|β﹣3|=3a+（﹣1）na（其中n∈N*、常数
），当n为奇数时，动点P（x、y）的轨迹为C1．当n为偶数时，动点P（x、y）的轨迹为C2．且两条曲线都经过点
，求轨迹C1与C2的方程；
（3）在（2）的条件下，轨迹C2上存在点A，使点A与点B（x0，0）（x0＞0）的最小距离不小于
，求实数x0的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】从中国教育在线官方公布的考研动机调查来看，本科生扎堆考研的原因大概集中在这6个方面：本科就业压力大，提升竞争力；通过考研选择真正感兴趣的专业；为了获得学历；继续深造；随大流；有名校情结.如图是2015～2019年全国硕士研究生报考人数趋势图（单位：万人）的拆线图.
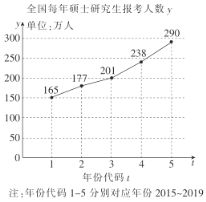
（1）求
关于
的线性回归方程；
（2）根据（1）中的回归方程，预测2021年全国硕士研究生报考人数.
参考数据：
；
回归方程
中斜率和截距的最小二乘估计公式分别为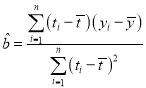
，
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
