
【题目】某林业部门为了保证植树造林的树苗质量,对甲、乙两家供应的树苗进行根部直径检测,现从两家供应的树苗中各随机抽取10株树苗检测,测得根部直径如下(单位:mm):
甲 | 27 | 11 | 21 | 10 | 19 | 09 | 22 | 13 | 15 | 23 |
乙 | 15 | 20 | 27 | 17 | 21 | 14 | 16 | 18 | 24 | 18 |

(1)画出甲、乙两家抽取的10株树苗根部直径的茎叶图,并根据茎叶图对甲、乙两家树苗进行比较,写出两个统计结论;
(2)设抽测的10株乙家树苗根部直径的平均值为![]() ,将这10株树苗直径依次输入程序框图中,求输出的S的值,并说明其统计学的意义.
,将这10株树苗直径依次输入程序框图中,求输出的S的值,并说明其统计学的意义.
科目:高中数学 来源: 题型:
【题目】南京江北新区是第十三个国家级新区,随着新区的经济发展,老城区将不断的进行开发和改造,如图为边长为4km的正三角形![]() 区域,
区域,![]() 分别在三边
分别在三边![]() 上,且
上,且![]() 为
为![]() 的中点,
的中点,![]() ,现将对正三角形
,现将对正三角形![]() 区域进行规划,规划
区域进行规划,规划![]() 区域为娱乐广场,其他区域为生活居住区.
区域为娱乐广场,其他区域为生活居住区.
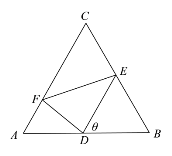
(1)若![]() ,求娱乐广场
,求娱乐广场![]() 的面积;
的面积;
(2)求生活区域的面积![]() 的最大值,并写出
的最大值,并写出![]() 取得最大值时
取得最大值时![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋中有6个球,其中4个白球,2个红球,从袋中任意取出两球,求下列事件的概率:
(1) 取出的两球1个是白球,另1个是红球;
(2) 取出的两球至少一个是白球。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】语音交互是人工智能的方向之一,现在市场上流行多种可实现语音交互的智能音箱,它们可以通过语音交互满足人们的部分需求.经市场调查,某种新型智能音箱的广告费支出x(万元)与销售额y(单位:万元)之间有如下对应数据:
x | 1 | 4 | 5 | 6 | 9 |
y | 20 | 35 | 50 | 65 | 80 |
(1)求y关于x的线性回归方程(数据精确到0.01);
(2)利用(1)中的回归方程,预测广告费支出10万元时的销售额.
附:回归直线的斜率和截距的最小二乘估计公式分别为: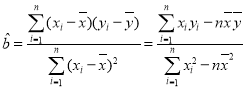 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义域为![]() 的函数
的函数![]() 满足:
满足:![]() ,且对于任意实数
,且对于任意实数![]() ,
,![]() 恒有
恒有![]() ,当
,当![]() 时,
时,![]() .
.
(1)求![]() 的值,并证明当
的值,并证明当![]() 时,
时,![]() ;
;
(2)判断函数![]() 在
在![]() 上的单调性并加以证明;
上的单调性并加以证明;
(3)若不等式![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2018届广东省汕头市高三上学期期末】某大型企业为鼓励员工多利用网络进行营销,准备为员工办理手机流量套餐.为了解员工手机流量使用情况,通过抽样,得到100位员工每人手机月平均使用流量![]() (单位:
(单位: ![]() )的数据,其频率分布直方图如下:
)的数据,其频率分布直方图如下:
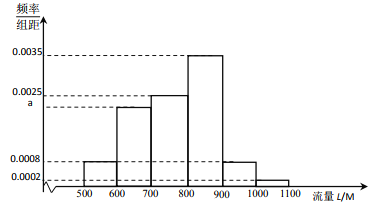
将频率视为概率,同一组中的数据用该组区间的中点值代替,回答以下问题:
(1) 求出![]() 的值,并计算这100位员工每月手机使用流量的平均值;
的值,并计算这100位员工每月手机使用流量的平均值;
(2) 据了解,某网络营运商推出两款流量套餐,详情如下:

流量套餐的规则是:每月1日收取套餐费。如果手机实际使用流量超出套餐流量,则需要购买流量叠加包,每一个叠加包(包含![]() 的流量)需要10元,可以多次购买;如果当月流量有剩余,将会被清零.
的流量)需要10元,可以多次购买;如果当月流量有剩余,将会被清零.
该企业准备订购其中一款流量套餐,每月为员工支付套餐费,以及购买流量叠加包所需月费用.若以平均费用为决策依据,该企业订购哪一款套餐更经济?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某翻译处有8名翻译,其中有小张等3名英语翻译,小李等3名日语翻译,另外2名既能翻译英语又能翻译日语,现需选取5名翻译参加翻译工作,3名翻译英语,2名翻译日语,且小张与小李恰有1人选中,则有____种不同选取方法.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com