
| A. | x2+4y2-2xy=3 | B. | x2+4y2+2xy=3 | C. | 4x2+y2-2xy=3 | D. | 4x2+y2+2xy=3 |
分析 根据已知条件利用余弦定理,求得对角线|$\overrightarrow{AC}$丨,根据向量加法和减法的三角形法则可得$\overrightarrow{AP}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$,两边平方即可求得结果.
解答 解:∵在平行四边形ABCD中,∠BAD=120°,AB=1,BC=AD=2,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}-2AB•BCcos∠ABC}$=$\sqrt{1+4-2×1×2×\frac{1}{2}}$=$\sqrt{3}$,
∵$\overrightarrow{OP}$=$\overrightarrow{OA}$+x$\overrightarrow{AB}$+y$\overrightarrow{AD}$,
∴$\overrightarrow{AP}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$,
∵点P在以A为圆心,|$\overrightarrow{AC}$丨为半径的圆上,
∴$\overrightarrow{AP}$2=(x$\overrightarrow{AB}$+y$\overrightarrow{AD}$)2,
即3=x2+4y2+2xy$\overrightarrow{AB}$•$\overrightarrow{AD}$=x2+4y2-2xy,
故选:A.
点评 此题考查余弦定理和向量的减法的三角形法则以及向量的数量积的定义,其中把已知条件化简为$\overrightarrow{AP}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$,是解题的关键,属中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
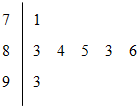 某学校2012年五四青年节举办十佳歌手赛,如图是七位评委为某选手打出的分数的茎叶图,去掉一个最高分和一个最低分后,所剩数据的众数数与中位数分别为( )
某学校2012年五四青年节举办十佳歌手赛,如图是七位评委为某选手打出的分数的茎叶图,去掉一个最高分和一个最低分后,所剩数据的众数数与中位数分别为( )| A. | 83,83 | B. | 83,83.5 | C. | 83,84 | D. | 84,83 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{1}{2}$,4] | B. | (-∞,-1]∪[2,+∞) | C. | [-1,2] | D. | (-∞,-2]∪[1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ¬p:?x0∈R,sinx0≥1 | B. | ¬p:?x∈R,sinx≥1 | ||
| C. | ¬p:?x0∈R,sinx0>1 | D. | ¬p:?x∈R,sinx>1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com