
(本小题满分13分)在△ABC中,角A,B,C所对的边分别为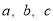 ,满足
,满足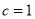 ,且
,且
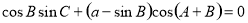 .
.
(1)求C的大小;
(2)求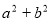 的最大值,并求取得最大值时角A,B的值.
的最大值,并求取得最大值时角A,B的值.
 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源:2014-2015学年浙江省高二上学期第二次月考数学试卷(解析版) 题型:选择题
直线x=1的倾斜角和斜率是 ( )
(A)45°,1 (B)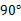 ,不存在
,不存在
(C)135°, -1 (D)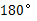 ,不存在
,不存在
查看答案和解析>>
科目:高中数学 来源:2014-2015学年河北省保定市高三上学期期末调研考试理科数学试卷(解析版) 题型:选择题
在区间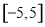 内随机取出一个实数
内随机取出一个实数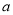 ,则
,则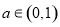 的概率为( )
的概率为( )
A.0.5 B.0.3 C.0.2 D.0.1
查看答案和解析>>
科目:高中数学 来源:2014-2015学年北京市东城区示范校高三上学期综合能力测试文科数学试卷(解析版) 题型:选择题
如图,直线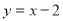 与圆
与圆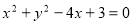 及抛物线
及抛物线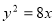 依次交于A、B、C、D四点,则
依次交于A、B、C、D四点,则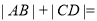 ( )
( )
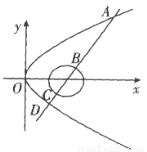
A. 13 B. 14 C. 15 D. 16
查看答案和解析>>
科目:高中数学 来源:2014-2015学年北京市东城区示范校高三上学期综合能力测试理科数学试卷(解析版) 题型:解答题
(本小题满分14分)给定正奇数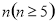 ,数列
,数列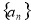 :
: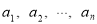 是1,2,…,
是1,2,…,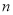 的一个排列,定义E(
的一个排列,定义E(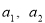 ,…,
,…,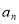 )
)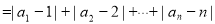 为数列
为数列 :
: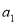 ,
, ,…,
,…,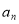 的位差和.
的位差和.
(1)当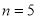 时,求数列
时,求数列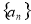 :1,3,4,2,5的位差和;
:1,3,4,2,5的位差和;
(2)若位差和E(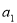 ,
,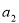 ,…,
,…,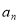 )=4,求满足条件的数列
)=4,求满足条件的数列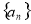 :
: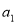 ,
,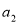 ,…,
,…,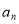 的个数;
的个数;
(3)若位差和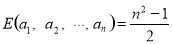 ,求满足条件的数列
,求满足条件的数列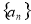 :
: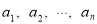 的个数.
的个数.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年北京市东城区示范校高三上学期综合能力测试理科数学试卷(解析版) 题型:填空题
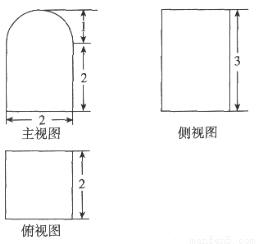
已知某个几何体的三视图如图(主视图中的弧线是半圆),根据图中标出的尺寸(单位: ),可得这个几何体的体积是__________
),可得这个几何体的体积是__________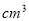 .
.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年北京市东城区示范校高三上学期综合能力测试理科数学试卷(解析版) 题型:选择题
设二项式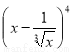 的展开式中常数项为A,则A=
的展开式中常数项为A,则A=
A. -6 B. -4 C. 4 D. 6
查看答案和解析>>
科目:高中数学 来源:2014-2015学年北京市大兴区高三上学期期末考试文科数学试卷(解析版) 题型:选择题
已知直线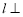 平面
平面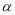 ,直线
,直线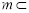 平面
平面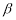 ,有下列四个命题:①若
,有下列四个命题:①若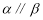 ,则
,则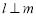 ;
;
②若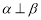 ,则
,则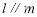 ;③若
;③若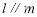 ,则
,则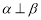 ;④若
;④若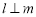 ,则
,则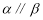 .
.
其中,正确命题的序号是
(A)①② (B)③④
(C)①③ (D)②④
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江苏省宿迁市高三上学期第一次摸底考试理科数学试卷(解析版) 题型:解答题
已知数列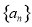 的各项均为正整数,对于任意n∈N*,都有
的各项均为正整数,对于任意n∈N*,都有 成立,且
成立,且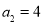 .
.
(1)求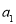 ,
,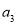 的值;
的值;
(2)猜想数列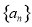 的通项公式,并给出证明.
的通项公式,并给出证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com