Question

12．正四面体ABCD中，棱AB与底面BCD所成角在余弦值是$\frac{\sqrt{3}}{3}$．

Answer 1

分析 在正四面体ABCD中，过A作AH⊥平面BCD于点H，则H为底面正三角形BCD的外心，连接BH，则∠ABH=α，就是AB与平面BCD所成角，解直角三角形ABH即可．

解答 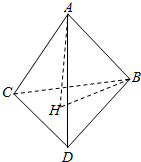解：正四面体ABCD，高为AH，
则H为底面正三角形BCD的外心，则∠ABH=α，就是AB与平面BCD所成角，
在Rt△ABH中，设棱长为a，
则BH=a×$\frac{\sqrt{3}}{2}$×$\frac{2}{3}$=$\frac{\sqrt{3}}{3}a$，AH=$\sqrt{{a}^{2}-（{\frac{\sqrt{3}}{3}a）}^{2}}$=$\frac{\sqrt{6}}{3}a$，
∴cosα=$\frac{HB}{AB}$=$\frac{\frac{\sqrt{3}}{3}a}{a}$=$\frac{\sqrt{3}}{3}$．
故答案为：$\frac{\sqrt{3}}{3}$．

点评 考查直线和平面所成的角，关键是找到斜线在平面内的射影，把空间角转化为平面角求解，属中档题．