
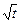 是函数f(x)=an-1x3-3[(t+1)an-an+1] x+1(n≥2)的
是函数f(x)=an-1x3-3[(t+1)an-an+1] x+1(n≥2)的 一个极值点.数列{an}中a1=t,a2=t2(t>0且t≠1) .
一个极值点.数列{an}中a1=t,a2=t2(t>0且t≠1) .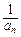 ),当t=2时,数列{bn}的前n项和为Sn,求使Sn>2010的n的最小值;
),当t=2时,数列{bn}的前n项和为Sn,求使Sn>2010的n的最小值;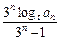 ,证明:
,证明: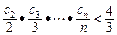 ( n∈N﹡).
( n∈N﹡).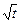 )=3an-1t-3[(t+1)an-an+1]=0.
)=3an-1t-3[(t+1)an-an+1]=0.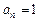 ;
;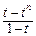 =tn-t,
=tn-t,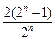 =2-
=2-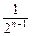 .
.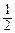 +
+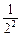 +…+
+…+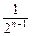 )=2n-
)=2n-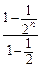
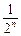 )=2n-2+2·
)=2n-2+2·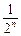
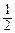 )n>2010, n+(
)n>2010, n+(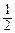 )n>1006,
)n>1006, 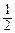 )n<1006,
)n<1006,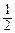 )n>1006,
)n>1006,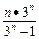 且c1=
且c1=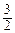 ,所以
,所以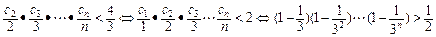 .
.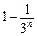 =
=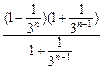 =
=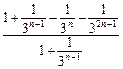
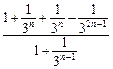 ≥
≥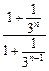 ,
,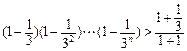
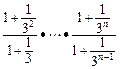 =
=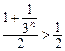 .
.

 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案科目:高中数学 来源:不详 题型:解答题
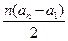 .
.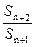 +
+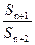 ,求数列﹛bn﹜的前n项和Tn;
,求数列﹛bn﹜的前n项和Tn;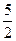 ,3)?若存在,证明你的结论,并给出一个具体的m值;若不存在,请说明理由。
,3)?若存在,证明你的结论,并给出一个具体的m值;若不存在,请说明理由。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
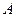 :
: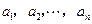 ,若满足
,若满足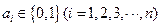 ,则称数列
,则称数列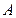 为“0-1
为“0-1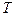 ,
,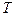 将“0-1数列”
将“0-1数列”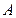 中原有的每个1都变成0,1,原有的每个0都变成1,0。例如
中原有的每个1都变成0,1,原有的每个0都变成1,0。例如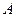 :1,0,1,则
:1,0,1,则 :
: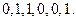 设
设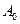 是“0-1数列”,令
是“0-1数列”,令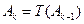 ,
,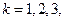 …。
…。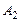 :
: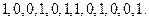 求数列
求数列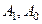 ;
;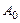 共有10项,则数列
共有10项,则数列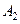 中连续两项
中连续两项 相等的数对至少有多少对?请说明理由;
相等的数对至少有多少对?请说明理由;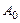 为0,1,记数列
为0,1,记数列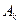 中连续两项都是0的数对
中连续两项都是0的数对 个数为
个数为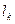 ,
,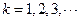 ,
,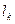 关于
关于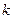 的表达式
的表达式查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com