
(本小题共13分)在等差数列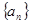 中,
中,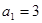 ,其前
,其前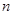 项和为
项和为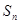 ,等比数列
,等比数列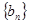 的各项均为正数,
的各项均为正数,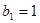 ,公比为
,公比为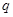 ,且
,且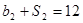 ,
,
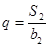 .
.
(Ⅰ)求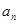 与
与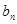 ;
;
(Ⅱ)数列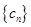 满足
满足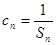 ,求
,求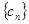 的前
的前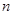 项和
项和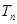 .
.
解:(Ⅰ)设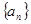 的公差为
的公差为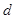 ,
,
因为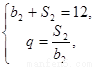 所以
所以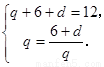
解得 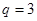 或
或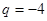 (舍),
(舍),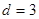 .
.
故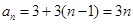 ,
,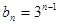 .
……………6分
.
……………6分
(Ⅱ)因为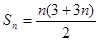 ,
,
所以
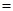
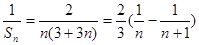 .
………11分
.
………11分
故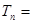
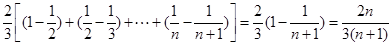 .……13分
.……13分
【解析】本题考查等差数列和等比数列的通项公式以及等比数列的前n项和,考查学生利用基本量思想和方程思想的解题能力。清晰数列的通项公式和求和公式联立方程求解是解决本类题目常用的解题思路,考查学生的计算能力。在数列求和问题中,由于题目的千变万化,使得不少同学一筹莫展,方法老师也介绍过,就不清楚什么特征用什么方法.为此提供一个通法 “特征联想法”:就是抓住数列的通项公式的特征,再去联想常用数列的求和方法.通项公式作为数列的灵魂,只有抓住它的特征,才能对号入座,得到求和方法.
特征一: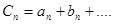 ,数列
,数列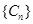 的通项公式能够分解成几部分,一般用“分组求和法”.特征二:
的通项公式能够分解成几部分,一般用“分组求和法”.特征二: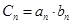 ,数列
,数列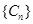 的通项公式能够分解成等差数列和等比数列的乘积,一般用“错位相减法”.特征三:
的通项公式能够分解成等差数列和等比数列的乘积,一般用“错位相减法”.特征三: ,数列
,数列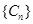 的通项公式是一个分式结构,一般采用“裂项相消法”.特征四:
的通项公式是一个分式结构,一般采用“裂项相消法”.特征四: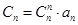 ,数列
,数列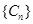 的通项公式是一个组合数和等差数列通项公式组成,一般采用“倒序相加法”.本题第二问采用裂项相消法求和。
的通项公式是一个组合数和等差数列通项公式组成,一般采用“倒序相加法”.本题第二问采用裂项相消法求和。


 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案科目:高中数学 来源:2011-2012学年北京市东城区高三上学期期末考试理科数学试卷(解析版) 题型:解答题
(本小题共13分)在等差数列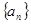 中,
中,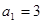 ,其前
,其前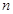 项和为
项和为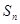 ,等比数列
,等比数列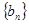 的各项均为正数,
的各项均为正数,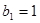 ,公比为
,公比为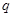 ,且
,且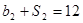 ,
,
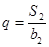 .
.
(Ⅰ)求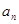 与
与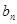 ;
;
(Ⅱ)证明: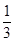 ≤
≤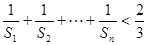 .
.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年北京市丰台区高三上学期期末考试理科数学 题型:解答题
.(本小题共13分)在平面直角坐标系xOy中,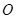 为坐标原点,动点
为坐标原点,动点 与两个定点
与两个定点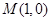 ,
, 的距离之比为
的距离之比为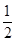 .
.
(Ⅰ)求动点 的轨迹
的轨迹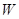 的方程;
的方程;
(Ⅱ)若直线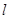 :
: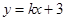 与曲线
与曲线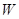 交于
交于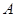 ,
,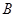 两点,在曲线
两点,在曲线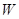 上是否存在一点
上是否存在一点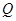 ,使得
,使得 ,若存在,求出此时直线
,若存在,求出此时直线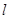 的斜率;若不存在,说明理由.
的斜率;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年北京市丰台区高三上学期期末考试文科数学 题型:解答题
(本小题共13分)在平面直角坐标系xOy中,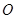 为坐标原点,以
为坐标原点,以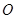 为圆心的圆与直线
为圆心的圆与直线 相切.
相切.
(Ⅰ)求圆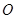 的方程;
的方程;
(Ⅱ)直线 :
: 与圆
与圆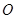 交于
交于 ,
, 两点,在圆
两点,在圆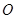 上是否存在一点
上是否存在一点 ,使得四边形
,使得四边形 为菱形,若存在,求出此时直线
为菱形,若存在,求出此时直线 的斜率;若不存在,说明理由.
的斜率;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年北京市房山区高三统练数学理卷 题型:解答题
(本小题共13分)
在平面直角坐标系 中,已知圆
中,已知圆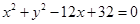 的圆心为
的圆心为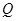 ,过点
,过点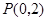 且斜率为
且斜率为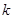 的直线
的直线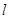 与圆
与圆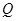 相交于不同的两点
相交于不同的两点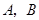 .
.
(Ⅰ)求圆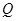 的面积;
的面积;
(Ⅱ)求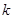 的取值范围;
的取值范围;
(Ⅲ)是否存在常数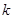 ,使得向量
,使得向量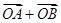 与
与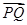 共线?如果存在,求
共线?如果存在,求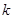 的值;如果不存在,请说
的值;如果不存在,请说
明理由.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年北京市丰台区高三下学期统一练习数学理卷 题型:解答题
(本小题共13分)
在△ABC中,a,b,c分别为内角A,B,C的对边,且b2+c2-a2=bc.
(Ⅰ)求角A的大小;
(Ⅱ)设函数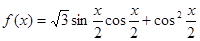 ,当
,当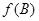 取最大值
取最大值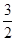 时,判断△ABC的形状.
时,判断△ABC的形状.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com