考点:棱柱、棱锥、棱台的体积,直线与平面垂直的判定
专题:空间位置关系与距离
分析:(1)利用直线与平面垂直的性质定理证明B1C1⊥BN,然后利用勾股定理证明BN⊥B1N,通过B1N∩B1C1=B1,利用直线与平面垂直的判定定理证明:BN⊥平面C1B1N;
(2)连接CN,说明NM⊥平面B1C1CB,然后五面体的体积V=VC-ABN+VN-B1C1CB分别求解即可.
解答:
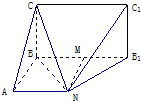
解:(1)证明:连4,过N作NM⊥BB
1,垂足为M,
∵B
1C
1⊥平面ABB
1N,BN?平面ABB
1N,
∴B
1C
1⊥BN,…(2分)
又,BC=4,AB=4,BM=AN=4,BA⊥AN,
∴
BN==4,
B1N===
4,
∵
BB1=82=64,B1N2+BN2=32+32=64,
∴BN⊥B
1N,…(4分)
∵B
1C
1?平面B
1C
1N,B
1N?平面B
1C
1N,B
1N∩B
1C
1=B
1∴BN⊥平面C
1B
1N…(6分)
(2)连接CN,
VC-ABN=×BC•S△ABN=×4××4×4=,…(8分)
又B
1C
1⊥平面ABB
1N,所以平面CBB
1C
1⊥平面ABB
1N,且平面CBB
1C
1∩ABB
1N=BB
1,NM⊥BB
1,
NM?平面B
1C
1CB,
∴NM⊥平面B
1C
1CB,…(9分)
VN-B1C1CB=×NM•S矩形B1C1CB=×4×4×8=…(11分)
此几何体的体积
V=VC-ABN+VN-B1C1CB=+=…(12分)
点评:本题考查直线与平面垂直的判定定理以及性质定理的应用,几何体的体积的求法,考查转化思想以及空间想象能力.

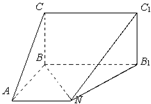 如图五面体中,四边形CBB1C1为矩形,B1C1⊥平面ABB1N,四边形ABB1N为梯形,
如图五面体中,四边形CBB1C1为矩形,B1C1⊥平面ABB1N,四边形ABB1N为梯形, 解:(1)证明:连4,过N作NM⊥BB1,垂足为M,
解:(1)证明:连4,过N作NM⊥BB1,垂足为M,

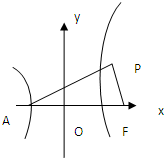 已知双曲线C的中心在原点,抛物线y2=8x的焦点是双曲线的一个焦点,且C过点
已知双曲线C的中心在原点,抛物线y2=8x的焦点是双曲线的一个焦点,且C过点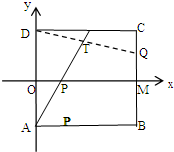 如图,矩形ABCD中,A(0,-1)D(0,1)B(2,-1)C(2,1),动点P在线段OM上运动,动点Q在线段CB上运动,保持|OP|=|CQ|,则直线AP与DQ的交点T的轨迹方程为
如图,矩形ABCD中,A(0,-1)D(0,1)B(2,-1)C(2,1),动点P在线段OM上运动,动点Q在线段CB上运动,保持|OP|=|CQ|,则直线AP与DQ的交点T的轨迹方程为