
[番茄花园1] 本题共有3个小题,第1小题满分3分,第2小题满分5分,第3小题满分10分。
若实数 、
、 、
、 满足
满足 ,则称
,则称 比
比 远离
远离 .
.
(1)若 比1远离0,求
比1远离0,求 的取值范围;
的取值范围;
(2)对任意两个不相等的正数 、
、 ,证明:
,证明: 比
比 远离
远离 ;
;
(3)已知函数 的定义域
的定义域 .任取
.任取 ,
, 等于
等于 和
和 中远离0的那个值.写出函数
中远离0的那个值.写出函数 的解析式,并指出它的基本性质(结论不要求证明).
的解析式,并指出它的基本性质(结论不要求证明).
23本题共有3个小题,第1小题满分3分,第2小题满分6分,第3小题满分9分.
已知椭圆 的方程为
的方程为 ,点P的坐标为(-a,b).
,点P的坐标为(-a,b).
(1)若直角坐标平面上的点M、A(0,-b),B(a,0)满足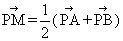 ,求点
,求点 的坐标;
的坐标;
(2)设直线 交椭圆
交椭圆 于
于 、
、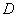 两点,交直线
两点,交直线 于点
于点 .若
.若 ,证明:
,证明: 为
为 的中点;
的中点;
(3)对于椭圆 上的点Q(a cosθ,b sinθ)(0<θ<π),如果椭圆
上的点Q(a cosθ,b sinθ)(0<θ<π),如果椭圆 上存在不同的两个交点
上存在不同的两个交点 、
、 满足
满足 ,写出求作点
,写出求作点 、
、 的步骤,并求出使
的步骤,并求出使 、
、 存在的θ的取值范围.
存在的θ的取值范围.
[番茄花园1]22.
[番茄花园1] 解析:(1) 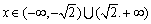 ;
;
(2) 对任意两个不相等的正数a、b,有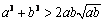 ,
,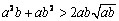 ,
,
因为 ,
,
所以 ,即a3+b3比a2b+ab2远离
,即a3+b3比a2b+ab2远离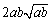 ;
;
(3)  ,
,
性质:1°f(x)是偶函数,图像关于y轴对称,2°f(x)是周期函数,最小正周期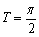 ,
,
3°函数f(x)在区间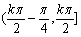 单调递增,在区间
单调递增,在区间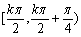 单调递减,kÎZ,
单调递减,kÎZ,
4°函数f(x)的值域为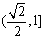 .
.
23解析:(1)  ;
;
(2) 由方程组 ,消y得方程
,消y得方程 ,
,
因为直线 交椭圆
交椭圆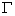 于
于 、
、 两点,
两点,
所以D>0,即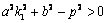 ,
,
设C(x1,y1)、D(x2,y2),CD中点坐标为(x0,y0),
则 ,
,
由方程组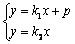 ,消y得方程(k2-k1)x=p,
,消y得方程(k2-k1)x=p,
又因为 ,所以
,所以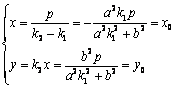 ,
,
故E为CD的中点;
(3) 求作点P1、P2的步骤:1°求出PQ的中点 ,
,
2°求出直线OE的斜率 ,
,
3°由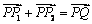 知E为CD的中点,根据(2)可得CD的斜率
知E为CD的中点,根据(2)可得CD的斜率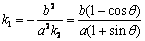 ,
,
4°从而得直线CD的方程: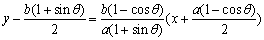 ,
,
5°将直线CD与椭圆Γ的方程联立,方程组的解即为点P1、P2的坐标.
欲使P1、P2存在,必须点E在椭圆内,
所以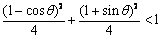 ,化简得
,化简得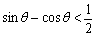 ,
,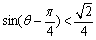 ,
,
又0<q <p,即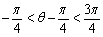 ,所以
,所以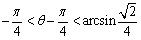 ,
,
故q 的取值范围是 .
.
[番茄花园1]22.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com