
【题目】如图,在斜三棱柱![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,均为正三角形,E为AB的中点.
,均为正三角形,E为AB的中点.
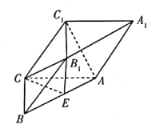
(1)证明:![]() 平面
平面![]() ,
,
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)如图,连接![]() ,交
,交![]() 于点M,连接ME,则
于点M,连接ME,则![]() ,再利用线面平行的判定定理,即可证明线面平行;
,再利用线面平行的判定定理,即可证明线面平行;
(2)设O是AC的中点,连接![]() ,OB,分别以射线OB,OA,
,OB,分别以射线OB,OA,![]() 的方向为x,y,z轴的正方向,建立空间直角坐标系,求出平面
的方向为x,y,z轴的正方向,建立空间直角坐标系,求出平面![]() 的一个法向量为
的一个法向量为![]() ,设直线
,设直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,代入公式
,代入公式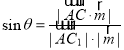 运算,即可得答案.
运算,即可得答案.
(1)如图,连接![]() ,交
,交![]() 于点M,连接ME,则
于点M,连接ME,则![]() .
.
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)设O是AC的中点,连接![]() ,OB.因为
,OB.因为![]() 为正三角形,
为正三角形,
所以![]() ,又平面
,又平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
所以![]() 平面ABC.由已知得
平面ABC.由已知得![]() .
.
如图,分别以射线OB,OA,![]() 的方向为x,y,z轴的正方向,建立空间直角坐标系,则有
的方向为x,y,z轴的正方向,建立空间直角坐标系,则有![]() ,
,![]() ,
,![]() ,
,![]() ,
,
故![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,则
,则 ,
,
所以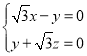 令
令![]() ,则
,则![]() .
.
设直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,
,
则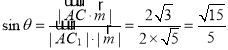 ,
,
故直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.



科目:高中数学 来源: 题型:
【题目】如图所示,一隧道内设双行线公路,其截面由一个长方形和抛物线构成.为保证安全,要求行使车辆顶部(设为平顶)与隧道顶部在竖直方向上的高度之差至少要有0.5米.若行车道总宽度AB为6米,则车辆通过隧道的限制高度是______米(精确到0.1米)

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合![]() ,集合
,集合![]() ,
,![]() ,
,![]() 满足.
满足.
①每个集合都恰有5个元素
②![]()
![]()
![]()
集合![]() 中元素的最大值与最小值之和称为集合
中元素的最大值与最小值之和称为集合![]() 的特征数,记为
的特征数,记为![]() ,则
,则![]()
![]()
![]() 的值不可能为( )
的值不可能为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国家统计局服务业调查中心和中国物流与采购联合会发布的2018年10月份至2019年9月份共12个月的中国制造业采购经理指数(PMI)如下图所示.则下列结论中错误的是( )
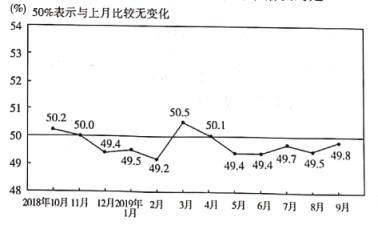
A.12个月的PMI值不低于50%的频率为![]()
B.12个月的PMI值的平均值低于50%
C.12个月的PMI值的众数为49.4%
D.12个月的PMI值的中位数为50.3%
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是定义在
是定义在![]() 上的函数,满足
上的函数,满足 .
.
(1)证明:2是函数![]() 的周期;
的周期;
(2)当![]() 时,
时,![]() ,求
,求![]() 在
在![]() 时的解析式,并写出
时的解析式,并写出![]() 在
在![]() (
(![]() )时的解析式;
)时的解析式;
(3)对于(2)中的函数![]() ,若关于x的方程
,若关于x的方程![]() 恰好有20个解,求实数a的取值范围.
恰好有20个解,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《算法统宗》全称《新编直指算法统宗》,是屮国古代数学名著,程大位著.书中有如下问题:“今有五人均银四十两,甲得十两四钱,戊得五两六钱.问:次第均之,乙丙丁各该若干?”意思是:有5人分40两银子,甲分10两4钱,戊分5两6钱,且相邻两项差相等,则乙丙丁各分几两几钱?(注:1两等于10钱)( )
A.乙分8两,丙分8两,丁分8两B.乙分8两2钱,丙分8两,丁分7两8钱
C.乙分9两2钱,丙分8两,丁分6两8钱D.乙分9两,丙分8两,丁分7两
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某基地蔬菜大棚采用水培、无土栽培方式种植各类蔬菜.过去50周的资料显示,该地周光照量![]() (小时)都在30小时以上,其中不足50小时的周数有5周,不低于50小时且不超过70小时的周数有35周,超过70小时的周数有10周.根据统计,该基地的西红柿增加量
(小时)都在30小时以上,其中不足50小时的周数有5周,不低于50小时且不超过70小时的周数有35周,超过70小时的周数有10周.根据统计,该基地的西红柿增加量![]() (百斤)与使用某种液体肥料
(百斤)与使用某种液体肥料![]() (千克)之间对应数据为如图所示的折线图.
(千克)之间对应数据为如图所示的折线图.

(1)依据数据的折线图,是否可用线性回归模型拟合![]() 与
与![]() 的关系?请计算相关系数
的关系?请计算相关系数![]() 并加以说明(精确到0.01).(若
并加以说明(精确到0.01).(若![]() ,则线性相关程度很高,可用线性回归模型拟合)
,则线性相关程度很高,可用线性回归模型拟合)
(2)蔬菜大棚对光照要求较大,某光照控制仪商家为该基地提供了部分光照控制仪,但每周光照控制仪最多可运行台数受周光照量![]() 限制,并有如下关系:
限制,并有如下关系:
周光照量 |
|
|
|
光照控制仪最多可运行台数 | 3 | 2 | 1 |
若某台光照控制仪运行,则该台光照控制仪周利润为3000元;若某台光照控制仪未运行,则该台光照控制仪周亏损1000元.若商家安装了3台光照控制仪,求商家在过去50周周总利润的平均值.
附:相关系数公式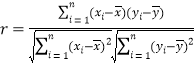 ,参考数据
,参考数据![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱![]() 中,
中,![]() 侧面
侧面![]() ,已知
,已知![]() ,
,![]() ,
,![]() ,点E是棱
,点E是棱![]() 的中点.
的中点.

(1)求证:![]() 平面ABC;
平面ABC;
(2)在棱CA上是否存在一点M,使得EM与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com