
| A. | -$\frac{1}{2}$ | B. | 0 | C. | $\frac{1}{2}$ | D. | 1 |
分析 利用二倍角公式降幂,再由两角差的正弦化积,结合x的范围得答案.
解答 解:f(x)=-$\sqrt{3}$sinxcosx-sin2x=$-\frac{\sqrt{3}}{2}sin2x-\frac{1-cos2x}{2}$
=$-(\frac{\sqrt{3}}{2}sin2x-\frac{1}{2}cos2x)-\frac{1}{2}$=$-sin(2x-\frac{π}{6})-\frac{1}{2}$.
∵$-\frac{π}{4}≤x≤\frac{π}{6}$,∴$-\frac{π}{2}≤2x≤\frac{π}{3}$,则$-\frac{2π}{3}≤2x-\frac{π}{6}≤\frac{π}{6}$,
∴当2x-$\frac{π}{6}$=$-\frac{π}{2}$时,$f(x)_{min}=1-\frac{1}{2}=\frac{1}{2}$.
故选:C.
点评 本题考查三角函数的最值,考查了两角和与差的正弦及二倍角公式的应用,是中档题.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
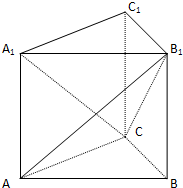 直三棱柱ABC-A1B1C1中,AC=BC=BB1=1,$A{B_1}=\sqrt{3}$.
直三棱柱ABC-A1B1C1中,AC=BC=BB1=1,$A{B_1}=\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | q<0 | B. | a2016a2018-1>0 | ||
| C. | T2016是数列{Tn}中的最大项 | D. | S2016>S2017 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com