
分析 由题意可得a、b为正数且b=$\frac{2}{a}$,代入化简可得原式=5+$\frac{2}{a}$+2a,由基本不等式可得.
解答 解:由题意可得a、b为正数且1=log2a-log${\;}_{\frac{1}{2}}$b=log2a+log2b=log2ab,
∴ab=2,∴b=$\frac{2}{a}$,∴(1+2a)(1+b)=(1+2a)(1+$\frac{2}{a}$)
=1+$\frac{2}{a}$+2a+4=5+$\frac{2}{a}$+2a≥5+2$\sqrt{\frac{2}{a}•2a}$=9
当且仅当$\frac{2}{a}$=2a即a=1且b2时取等号.
故答案为:9.
点评 本题考查基本不等式求最值,涉及对数的运算,属基础题.


科目:高中数学 来源:2016-2017学年江西上高县二中高二文9月月考数学文试卷(解析版) 题型:选择题
如下图,能推断这个几何体可能是三棱台的是( )

A. ,
, ,
, ,
,
B. ,
, ,
, ,
, ,
, ,
,
C. ,
, ,
, ,
, ,
, ,
,
D. ,
, ,
,
查看答案和解析>>
科目:高中数学 来源:2015-2016学年四川成都石室中学高二理下期中数学试卷(解析版) 题型:选择题
如图,网格纸上正方形小格的边长为 ,图中粗线画出的是某几何体的三视图,则几何体的体积为( )
,图中粗线画出的是某几何体的三视图,则几何体的体积为( )

A.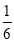 B.
B.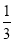 C.
C.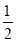 D.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m恒为负数 | |
| B. | 当d>0时,m恒为正数;当d<0时,m恒为负数 | |
| C. | m恒为正数 | |
| D. | 当d>0时,m恒为负数;当d<0时,m恒为正数 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
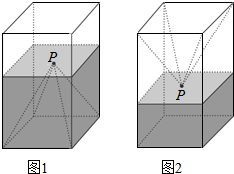 如图1,一个正四棱柱形的密闭容器水平放置,其底部镶嵌了同底的正四棱锥形实心装饰块,容器内盛有a升水时,水面恰好经过正四棱锥的顶点P.如果将容器倒置,水面也恰好过点P(图2).有下列四个结论,其中错误的代号是( )
如图1,一个正四棱柱形的密闭容器水平放置,其底部镶嵌了同底的正四棱锥形实心装饰块,容器内盛有a升水时,水面恰好经过正四棱锥的顶点P.如果将容器倒置,水面也恰好过点P(图2).有下列四个结论,其中错误的代号是( )| A. | 若往容器内再注入a升水,则容器恰好能装满 | |
| B. | 将容器侧面水平放置时,水面也恰好过点P | |
| C. | 任意摆放该容器,当水面静止时,水面都恰好经过点P | |
| D. | 正四棱锥的高等于正四棱柱高的一半 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com