
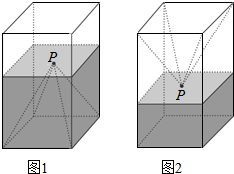
 ��ͼ1��һ�����������ε��ܱ�����ˮƽ���ã���ײ���Ƕ��ͬ����������ʵ��װ�ο飬������ʢ��a��ˮʱ��ˮ��ǡ�þ����������Ķ���P��������������ã�ˮ��Ҳǡ�ù���P��ͼ2�����������ĸ����ۣ����д���Ĵ����ǣ�������
��ͼ1��һ�����������ε��ܱ�����ˮƽ���ã���ײ���Ƕ��ͬ����������ʵ��װ�ο飬������ʢ��a��ˮʱ��ˮ��ǡ�þ����������Ķ���P��������������ã�ˮ��Ҳǡ�ù���P��ͼ2�����������ĸ����ۣ����д���Ĵ����ǣ�������| A�� | ������������ע��a��ˮ��������ǡ����װ�� | |
| B�� | ����������ˮƽ����ʱ��ˮ��Ҳǡ�ù���P | |
| C�� | ����ڷŸ���������ˮ�澲ֹʱ��ˮ�涼ǡ�þ�����P | |
| D�� | �������ĸߵ������������ߵ�һ�� |
���� �������⣬��ͼ1��ˮ�ĸ߶�Ϊh2��������ĸ�Ϊh1�����������εı߳�Ϊb������ˮ��������ó�h1��h2�Ĺ�ϵ���Ӷ��ж�D����A��B��C��ȷ��
��� �⣺��ͼ1��ˮ�ĸ߶�h2��������ĸ�Ϊh1�����������εı߳�Ϊb��
��ͼ2��ˮ�����Ϊb2h1-b2h2=b2��h1-h2����
��$\frac{2}{3}$b2h2=b2��h1-h2�������h1=$\frac{5}{3}$h2��
�����������ĸߵ������������ߵ�һ���Ǵ���ģ���D����
����A������������ע��a��ˮ��ˮ�潫����$\frac{2}{3}$h2����h2+$\frac{2}{3}$h2=$\frac{5}{3}$h2=h1������ǡ����װ����A��ȷ��
����B������������ˮƽ����ʱ��P���ڳ������н����ϣ�ռ�����ڿռ��һ�룬
����ˮ��Ҳǡ�þ���P�㣬B��ȷ��
����C������ڷŸ���������ˮ�澲ֹʱ��P���ڳ������н����ϣ�ʼ��ռ�����ڿռ��һ�룬
����ˮ�涼ǡ�þ�����P��C��ȷ��
��ѡ��D��
���� ���⿼�鼸��ģ�͵�Ӧ�����⣬Ҳ�����˿ռ伸��������Ӧ�����⣬����ʱҪ�������⣬ע��ռ�˼ά������Ӧ�ã����ۺ�����Ŀ��


 ���Ž�������С״Ԫϵ�д�
���Ž�������С״Ԫϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0�� | B�� | 1�� | C�� | 2�� | D�� | ������ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y=$��\sqrt{2}$x | B�� | y=��$\frac{\sqrt{7}}{3}$x | C�� | y=��$\frac{4}{3}$x | D�� | y=��$\sqrt{6}$x |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
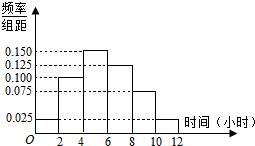 ijУ����ѧ��1600�ˣ���������1000�ˣ�Ů��600�ˣ�Ϊ�����Уѧ��ÿ��ƽ�������˶�ʱ�����������÷ֲ�����ķ������ռ�40λѧ��ÿ��ƽ�������˶�ʱ����������ݣ���λ��Сʱ����
ijУ����ѧ��1600�ˣ���������1000�ˣ�Ů��600�ˣ�Ϊ�����Уѧ��ÿ��ƽ�������˶�ʱ�����������÷ֲ�����ķ������ռ�40λѧ��ÿ��ƽ�������˶�ʱ����������ݣ���λ��Сʱ�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {3} | B�� | {2��3} | C�� | {2} | D�� | {2��3��4} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | 1 | B�� | -1 | C�� | -2 | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 8x+6y+13=0 | B�� | 6x-8y+13=0 | C�� | 4x+3y+13=0 | D�� | 3x+4y+26=0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com