
分析 由已知得$\left\{\begin{array}{l}{{x}_{1}=a+{t}_{1}cosθ}\\{{y}_{1}=b={t}_{1}sinθ}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=a+{t}_{2}cosθ}\\{{y}_{2}=a+{t}_{2}sinθ}\end{array}\right.$,从而运动质点从时间t1到t2经过的距离|M1M2|=$\sqrt{({x}_{1}-{x}_{2})^{2}+({y}_{1}-{y}_{2})^{2}}$,由此能求出结果.
解答 解:∵质点运动的轨迹方程为$\left\{\begin{array}{l}{x=a+tcosθ}\\{y=b+tsinθ}\end{array}\right.$(t为参数),
∴$\left\{\begin{array}{l}{{x}_{1}=a+{t}_{1}cosθ}\\{{y}_{1}=b={t}_{1}sinθ}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=a+{t}_{2}cosθ}\\{{y}_{2}=a+{t}_{2}sinθ}\end{array}\right.$,
∴M1(a+t1cosθ,b+t1sinθ),M2(a+t2cosθ,b+t2sinθ),
∴|M1M2|=$\sqrt{({x}_{1}-{x}_{2})^{2}+({y}_{1}-{y}_{2})^{2}}$
=$\sqrt{({t}_{1}-{t}_{2})^{2}(co{s}^{2}α+si{n}^{2}α)}$
=|t1-t2|.
∴运动质点从时间t1到t2经过的距离为|t1-t2|.
点评 本题考查质点运动距离的求法,是基础题,解题时要认真审题,注意两点间距离公式的合理运用.


科目:高中数学 来源:2016-2017学年江西上高县二中高二文9月月考数学文试卷(解析版) 题型:解答题
如图,在直三棱柱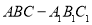 中,
中,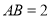 ,
, ,
,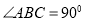 .
.

(1)求三棱柱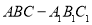 的表面积S;
的表面积S;
(2)求异面直线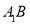 与
与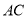 所成角的余弦值.
所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源:2015-2016学年四川成都石室中学高二理下期中数学试卷(解析版) 题型:选择题
已知动点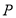 到点
到点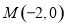 和到直线
和到直线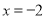 的距离相等,则动点
的距离相等,则动点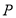 的轨迹是( )
的轨迹是( )
A.抛物线 B.双曲线左支
C.一条直线 D.圆
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 无数个 | B. | 6个 | C. | 4个 | D. | 0个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=$±\sqrt{2}$x | B. | y=±$\frac{\sqrt{7}}{3}$x | C. | y=±$\frac{4}{3}$x | D. | y=±$\sqrt{6}$x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com